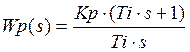 , где
, где ![]() и
и ![]()
Передаточную функцию системы находят как произведение передаточных функ-ций
объекта и регулятора, т.е. ![]() .
.
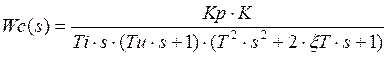
Пусть ![]() тогда
тогда 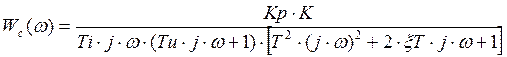
Значит, АЧХ имеет вид: ![]()
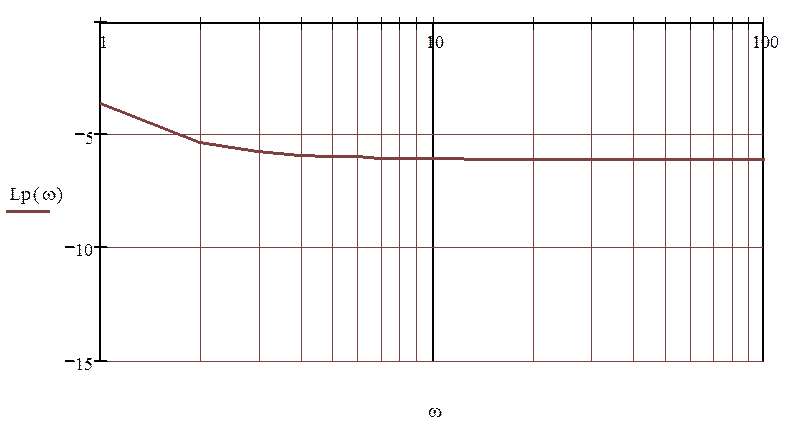
Характеристика при коэффициенте передачи регулятора Кр = 1:
ЛАЧХ имеет вид: ![]()
ЛФЧХ имеет вид:
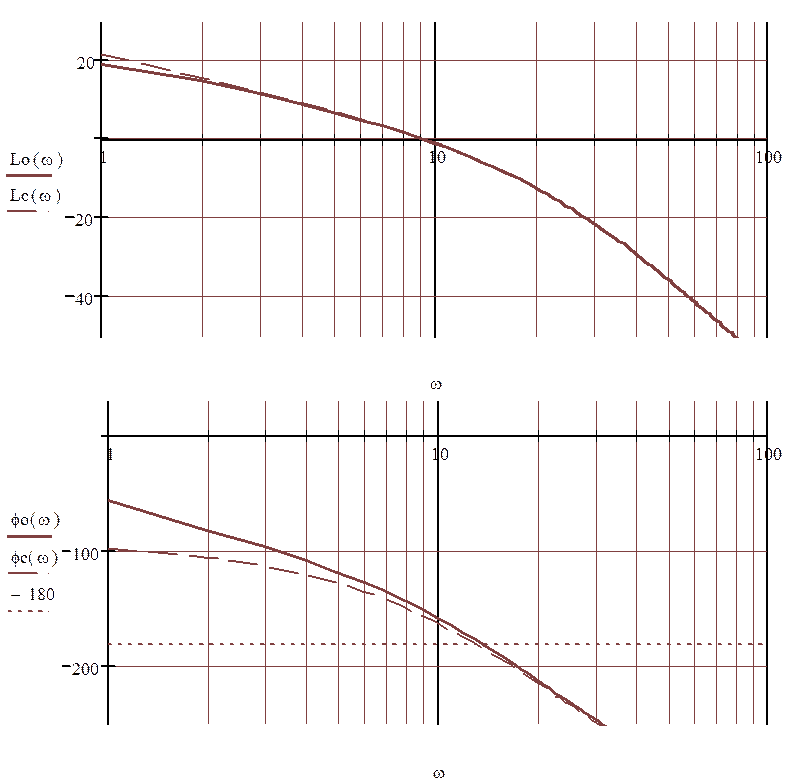
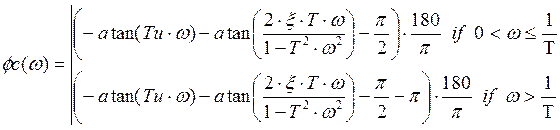
Рисунок 2.1.1 - ЛАЧХ и ЛФЧХ объекта регулирования ( располагаемая характеристика) и системы с коэффициентом передачи регулятора Кр = 1.
По графику представленному в [3, с.272, рис.5.24], учитывая, что s = 24% определяют Pmax:
![]()
По графику представленному в [3, с.273, рис.5.25], используя Pmax находят заданный запас по модулю и по фазе:
![]()
![]()
Находят частоту среза,
решая уравнение: ![]()
![]()
![]()
При ![]() , тогда
, тогда ![]() ,
откуда
,
откуда 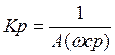
![]()
![]()
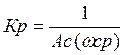
Проверка: ![]()
Таким образом, коэффициентом передачи
ПИ-регулятора равен: ![]()
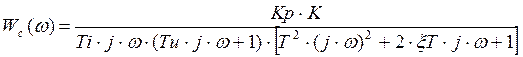 -
Передаточная функция
-
Передаточная функция
системы при Кр = 0.498
![]() - АЧХ системы
- АЧХ системы
ЛАЧХ и ЛФЧХ системы с заданными параметрами регулирования :
![]()
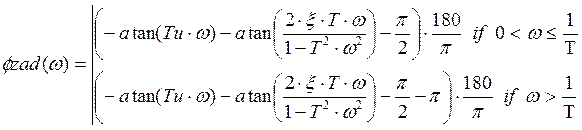
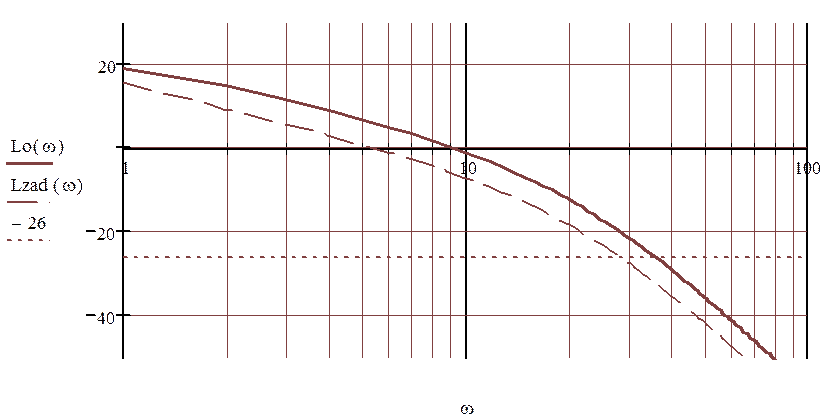
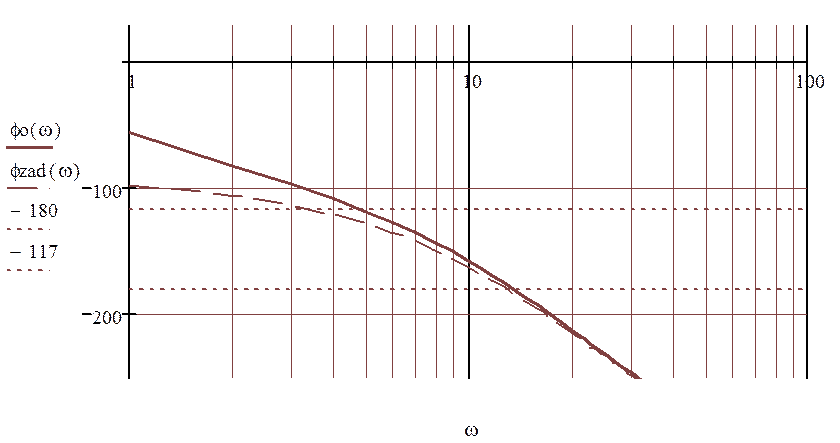
Рисунок 2.1.2 - ЛАЧХ и ЛФЧХ объекта регулирования(располагаемая характеристика) и системы с заданными параметрами регулирования.
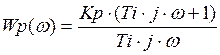
![]() - ЛАЧХ регулятора.
- ЛАЧХ регулятора.
Рисунок 2.1.3 - ЛАЧХ регулятора
2.2 Переходные характеристики.
2.2.1 В замкнутой системе по управляющему воздействию.
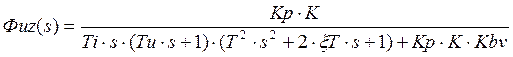
Для нахождения переходной функции используется обратное преобразование Лапласа: hz(t)=L^(-1){Ф(s)/s}
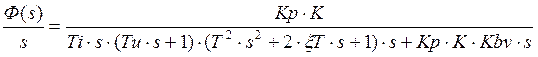
Имеем характеристическое уравнение:
![]() , где
, где
![]()
![]()
![]()
![]()
![]()
Тогда, ![]()
![]()
Найдём корни характеристического уравнения:
![]()
![]()
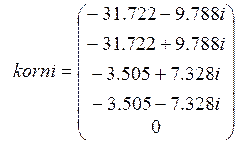
![]()
![]()
![]()
![]()
![]()
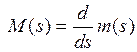
![]()
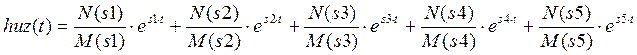
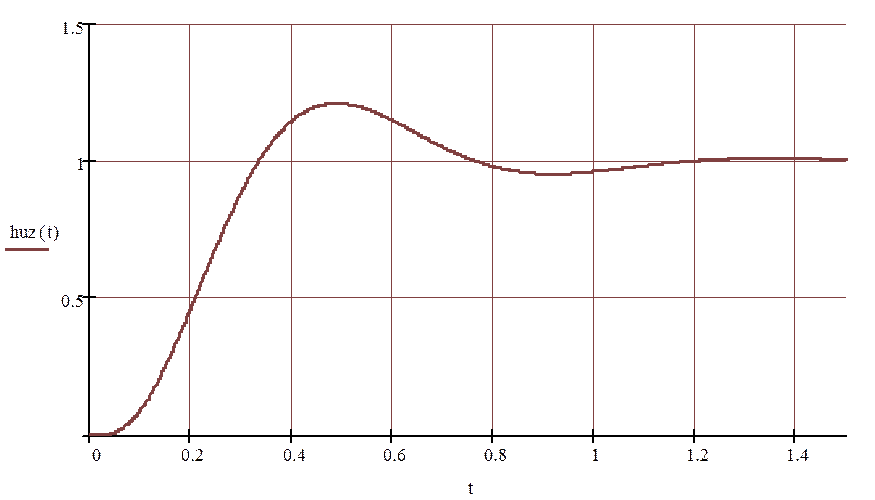
Рисунок 2.2.1.1 - Переходная характеристика в замкнутой системе по управляющему воздействию.
2.2.2 В замкнутой системе по возмущающему воздействию.
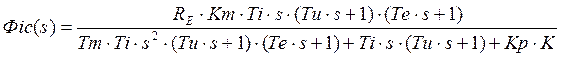
Для нахождения переходной функции используется обратное преобразование Лапласа: hz(t)=L^(-1){Ф(s)/s}
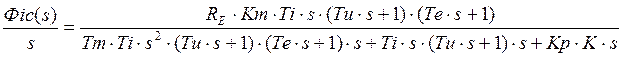
Имеем характеристическое уравнение:
![]() , где
, где
![]()
![]()
![]()
![]()
![]()
Тогда, ![]()
![]()
Найдём корни характеристического уравнения:
![]()
![]()
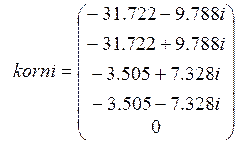
![]()
![]()
![]()
![]()
![]()
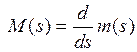
![]()
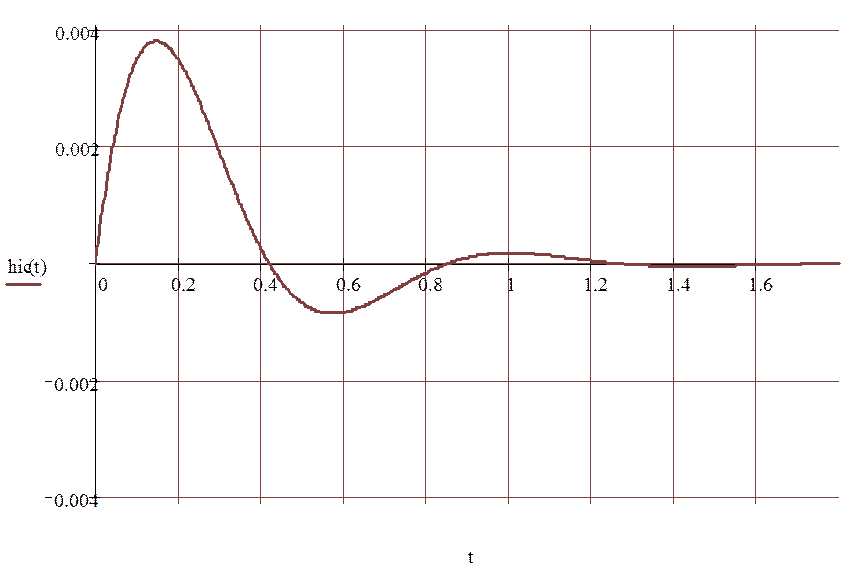
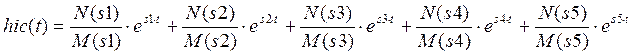
Рисунок 2.2.2.1 - Переходная характеристика в замкнутой системе по возмущающему воздействию.
3 Оптимизация САУ по критерию параметрической стабилизации.
3.1 Расчёт необходимых настроек регулятора по заданным параметрам регулирования.
![]()
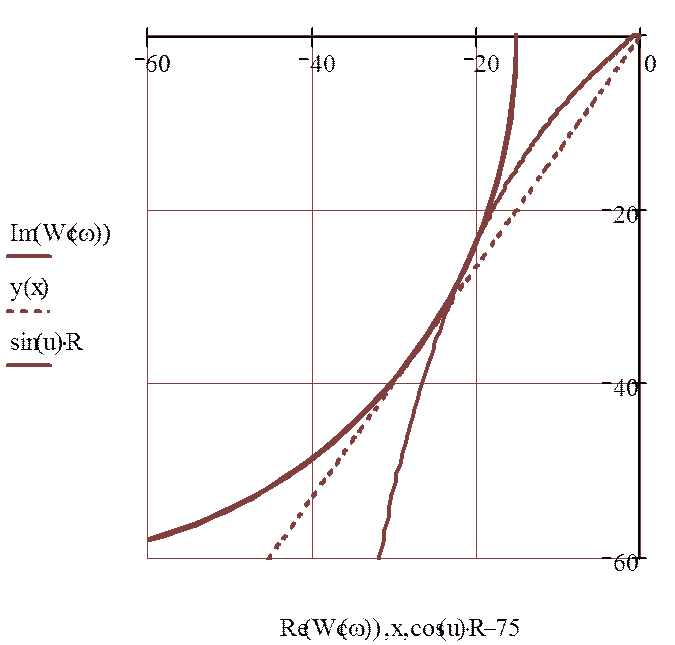
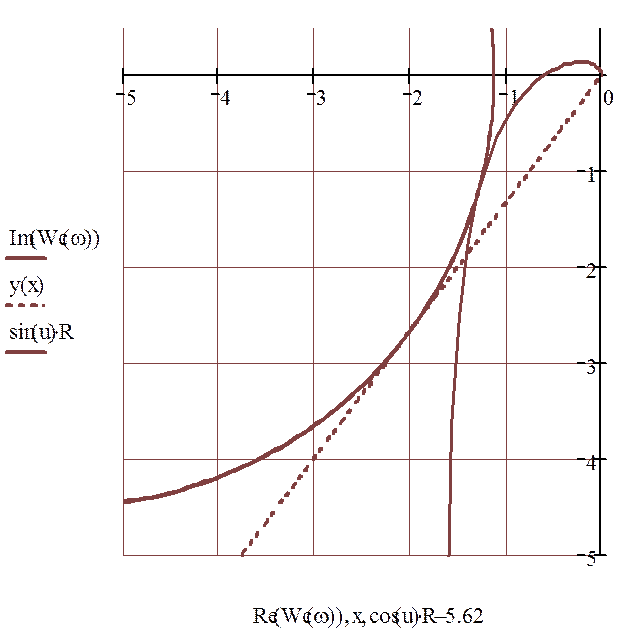
Строится семейство КФЧХ разомкнутой системы, при коэффициенте передачи ре-
гулятора
(![]() ) и нескольких значений Ti. Затем,
путём подбора, строятся окружно-
) и нескольких значений Ti. Затем,
путём подбора, строятся окружно-
сти с центром на отрицательном участке вещественной оси и касающиеся одновре-
менно
КФЧХ и луча, проведенного через начало координат под углом 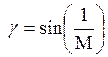 к вещественной оси.
к вещественной оси.
Коэффициент передачи регулятора, обеспечивающий заданный показатель колеба
тельности М определяется по выражению:
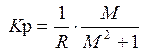
где R - радиус окружности.
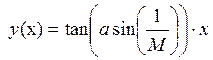 - уравнение луча, проведенного через начало координат
под
- уравнение луча, проведенного через начало координат
под
углом
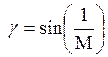 к вещественной оси.
к вещественной оси.
![]()
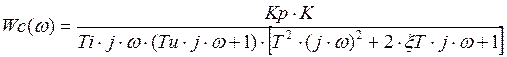
Радиус окружности равен: ![]()
Тогда, ![]()
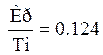
![]()
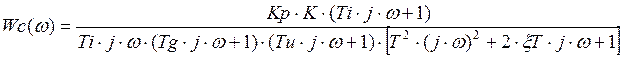
|
|
Радиус окружности равен: ![]()
Тогда, ![]()
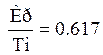
![]()
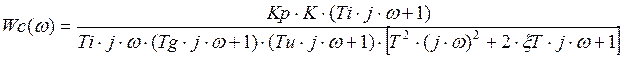
|
|
Радиус окружности равен: ![]()
Тогда, ![]()
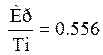
![]()
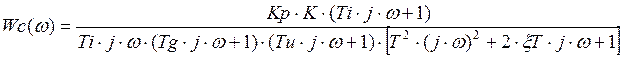
|
|
Радиус окружности равен: ![]()
Тогда, ![]()
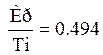
![]()
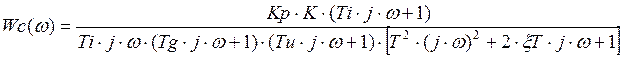
Радиус окружности
равен: ![]()
Тогда, ![]()
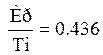
Таким
образом, 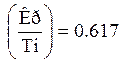 то есть
то есть ![]()
![]() являются оптимальными.
являются оптимальными.
Строим график зависимости Кр/Тi=f(Тi) для определения оптимальных параметров.
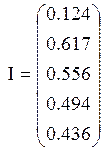
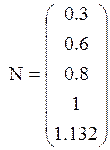
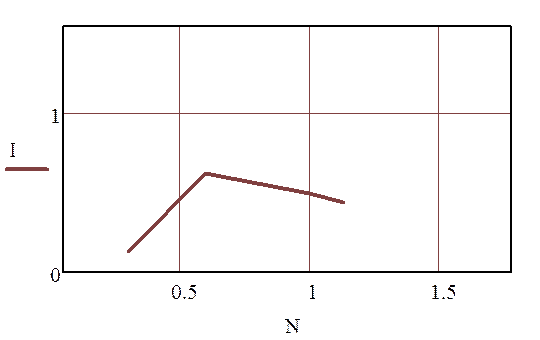
Рисунок 3.1.1- График зависимости Кр/Тi=f(Тi)
3.2 Переходные характеристики.
3.2.1 В замкнутой системе по управляющему воздействию.
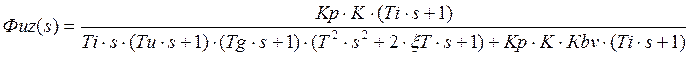
Для нахождения переходной функции используется обратное преобразование Лапласа: hz(t)=L^(-1){Ф(s)/s}
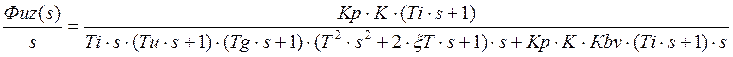
Имеем характеристическое уравнение:
![]() , где
, где
![]()
![]()
![]()
![]()
![]()
![]()
Тогда, ![]()
![]()
Найдём корни характеристического уравнения:
![]()
![]()
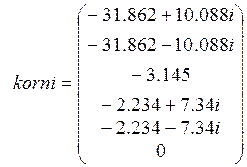
![]()
![]()
![]()
![]()
![]()
![]()
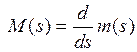
![]()
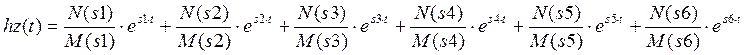
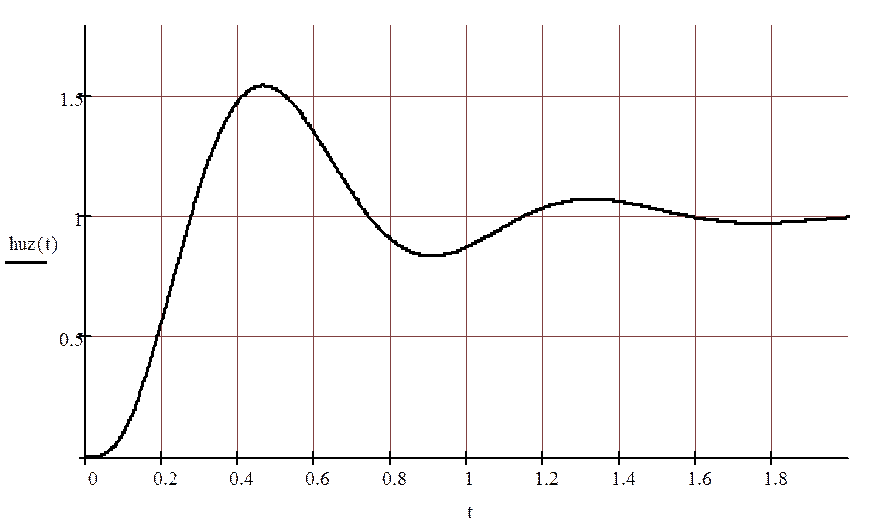
Рисунок 3.2.2.1 - Переходная характеристика в замкнутой системе по управляющему воздействию.
3.2.2 В замкнутой системе по возмущающему воздействию.
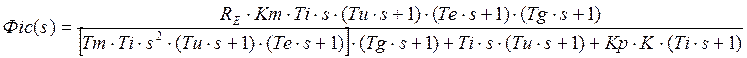
Для нахождения переходной функции используется обратное преобразование Лапласа: hz(t)=L^(-1){Ф(s)/s}
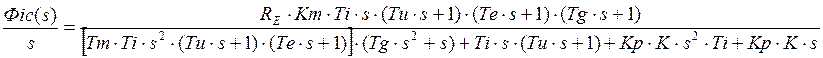
Имеем характеристическое уравнение:
![]() , где
, где
![]()
![]()
![]()
![]()
![]()
![]()
Тогда, ![]()
![]()
Найдём корни характеристического уравнения:
![]()
![]()
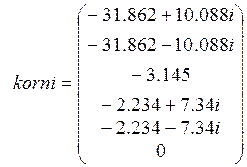
![]()
![]()
![]()
![]()
![]()
![]()
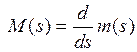
![]()
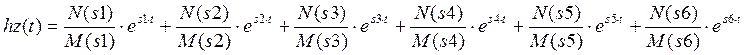
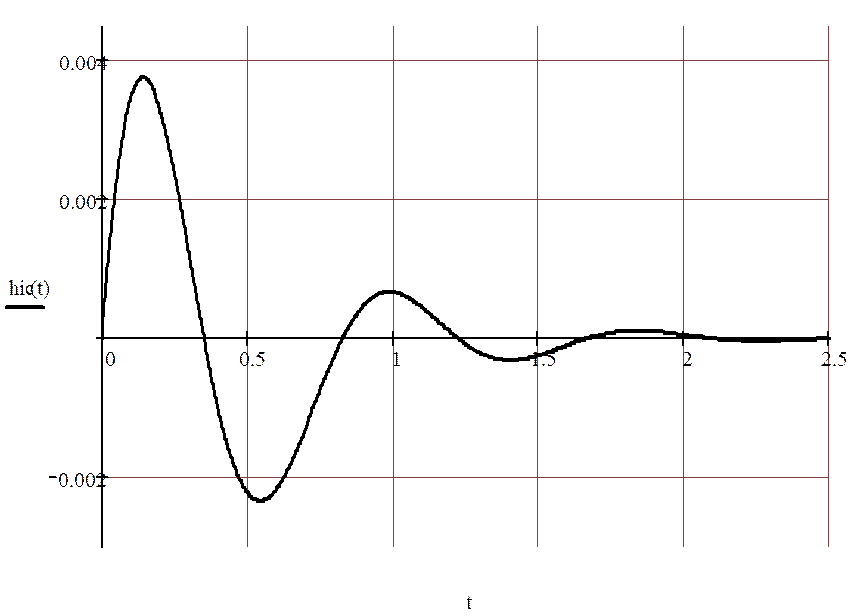
Рисунок 3.2.3.1 - Переходная характеристика в замкнутой системе по возмущающему воздействию.
4 Схемная реализация регулятора скорости и расчёт его параметров.
При расчёте RC-цепей первоначально задаются значением С, а затем определяют величину R. Пределы изменения данных параметров следующие:
С = (1 - 5) мкФ;
R = (10 - 500) кОm.
Пусть, ![]() , тогда. Примем
, тогда. Примем ![]()
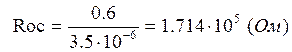
Затем по известному значению коэффициента передачи
регулятора определяют ![]() .
.
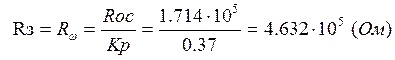
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.