1.3.2 Передаточная функция и дифференциальное уравнение замкнутой системы по возмущающему воздействию.
Структурная схема замкнутой системы по возмущающему воздействию представлена в Приложении В. Рисунок В.3
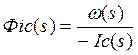 при
при ![]()
![]()
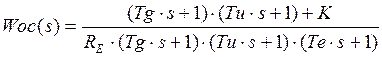
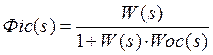
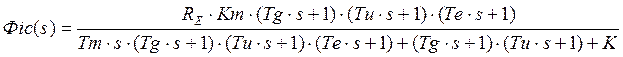
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Дифференциальное уравнение имеет вид:
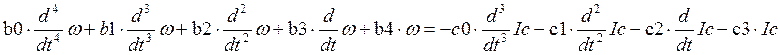
1.3.3 Передаточная функция и дифференциальное уравнение замкнутой системы по ошибке.
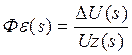
![]()
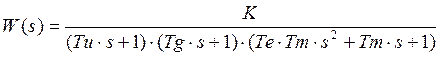
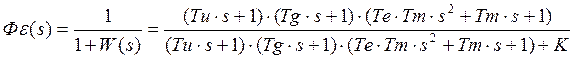
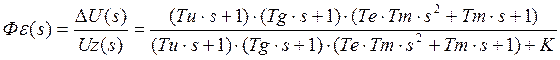
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Дифференциальное уравнение имеет вид:
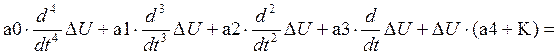
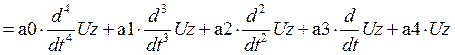
1.3.4 Передаточная функция и дифференциальное уравнение разомкнутой системы.
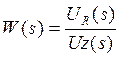
![]()
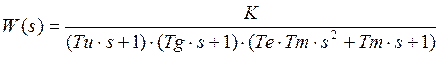
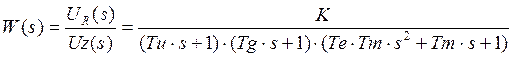
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Дифференциальное уравнение имеет вид:
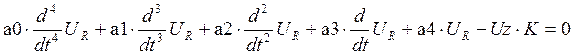
1.4 Анализ устойчивости, определение критического коэффициента усиления, используя критерий Михайлова.
![]()
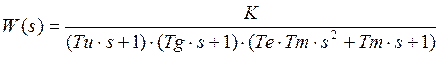 -разомкнутая
система
-разомкнутая
система
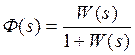
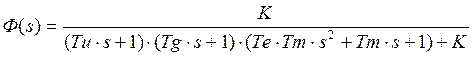 -замкнутая
система
-замкнутая
система
![]() -
характеристическое уравнение
-
характеристическое уравнение
![]()
![]()
![]()
![]()
![]()
![]()
Исследование замкнутой системы на устойчивость методом частотного критерия Михайлова производится исходя из знаменателя передаточной функции замкнутой системы. Необходимо построить кривую Михайлова - годограф характеристического уравнения:
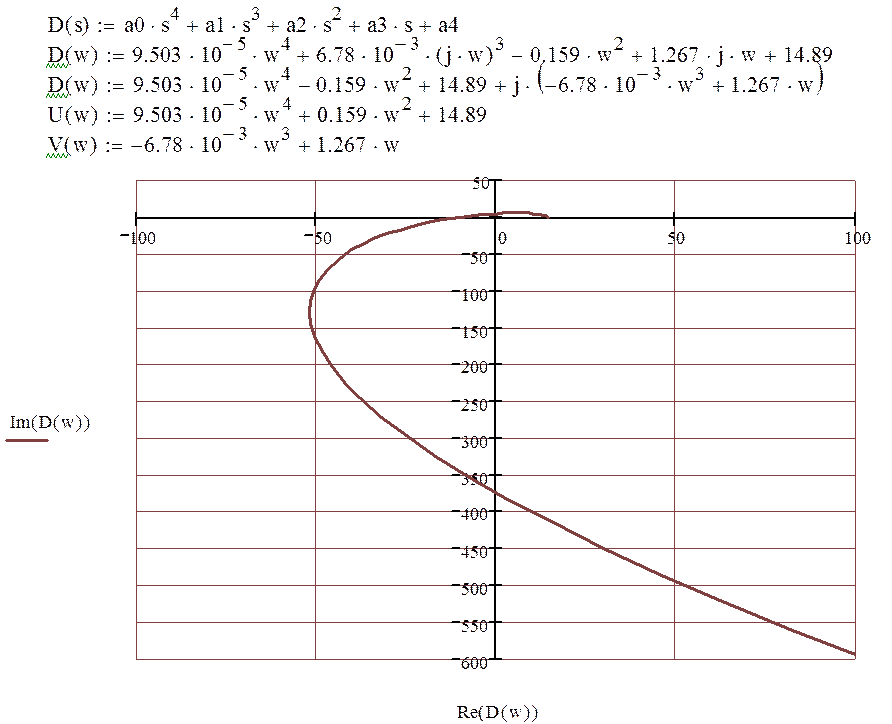
Критический коэффициент усиления системы равен:
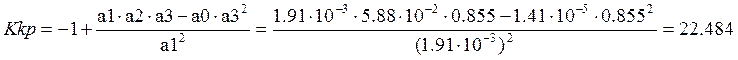
1.5 Построение ЛАЧХ и ЛФЧХ разомкнутой системы. Оценка качества регулирования в замкнутой и разомкнутой системе.
Так как 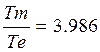 , т.е.
, т.е. 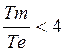 , то
, то 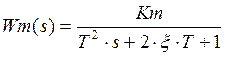 , где
, где
![]()
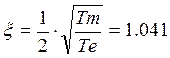 .Тогда передаточная функция разомкнутой системы примет
вид:
.Тогда передаточная функция разомкнутой системы примет
вид:
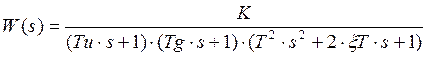
Пусть ![]() тогда:
тогда:
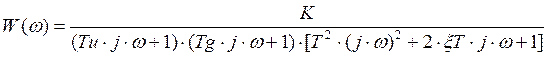
Значит, АЧХ имеет вид: ![]()
ЛАЧХ имеет вид: ![]()
 ЛФЧХ
имеет вид:
ЛФЧХ
имеет вид: 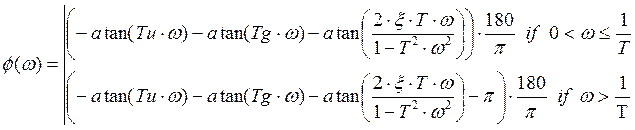
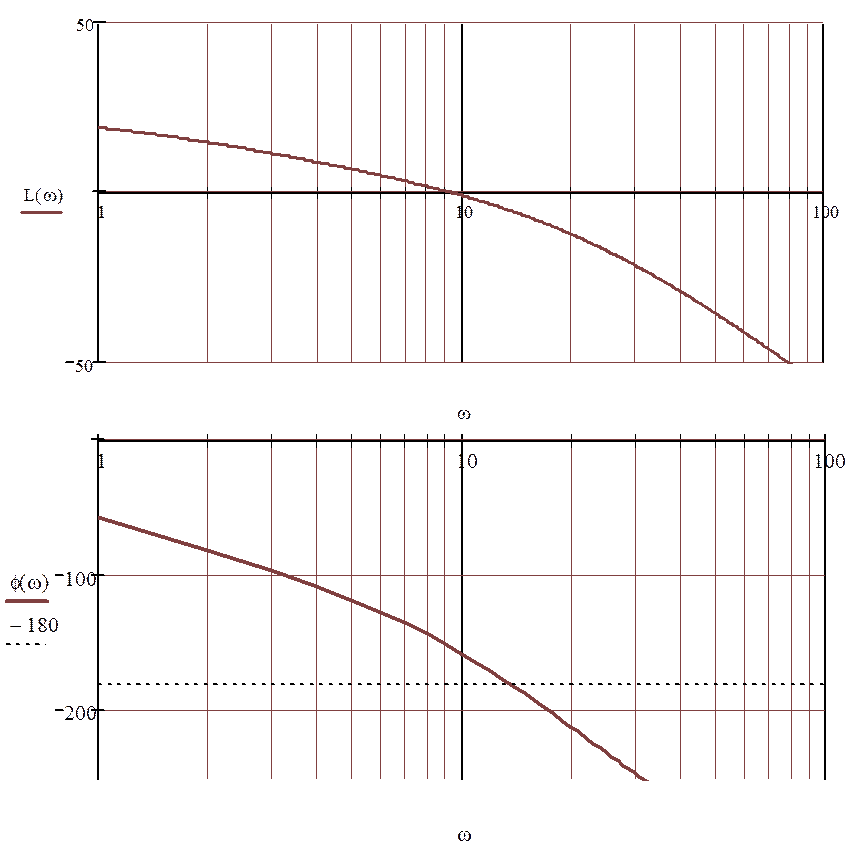
Рисунок 1.5.1 - ЛАЧХ и ЛФЧХ разомкнутой системы.
По ЛАЧХ определяют ![]() :
:
![]()
По ЛФЧХ определяют wкр: ![]()
Затем определяют запас по модулю и по фазе (![]() ;
; ![]() ):
):
![]() -
запас по фазе
-
запас по фазе
![]() -
запас по модулю
-
запас по модулю
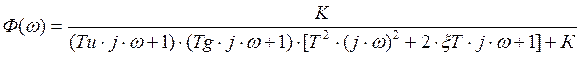 -замкнутая
система
-замкнутая
система
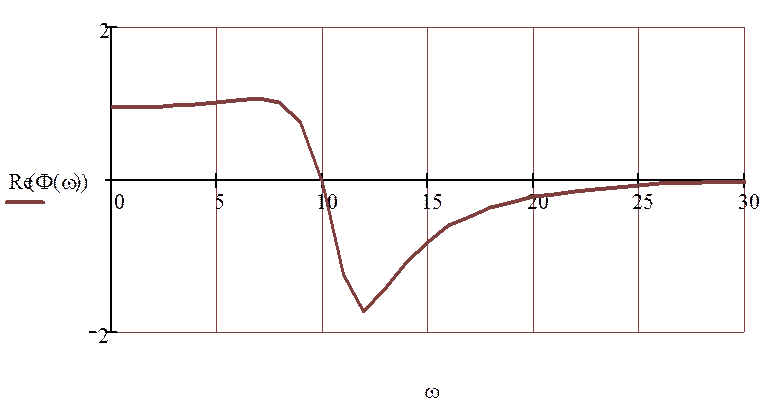
Рисунок 1.5.2 - ВЧХ замкнутой системы.
По графику представленному в [3, с.273, рис.5.25] определяют Pmax:
![]()
По графику представленному в [3, с.272, рис.5.24] определяют время регулирования в замкнутой системе tp:
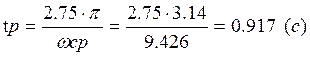
Время регулирования в разомкнутой системе оценивают по корням характеристи-ческого уравнения разомкнутой системы, считая, что tp = 4/si, где si - наименьший корень характеристического уравнения.
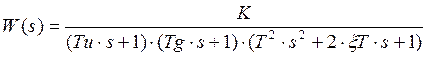
![]() -
характеристическое уравнение
-
характеристическое уравнение
![]()
где
![]()
![]()
![]()
![]()
![]()
Найдём корни характеристического уравнения:
![]()
![]()
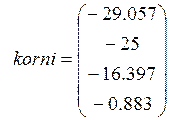
![]()
![]()
![]()
![]()
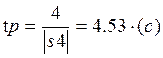
Время регулирования в разомкнутой системе равно: ![]()
Переходные характеристики в разомкнутой и замкнутой системе:
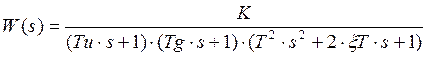 -разомкнутая
система
-разомкнутая
система
Для нахождения переходной функции используется обратное преобразование Лапласа:
hp(t)=L^(-1){W(s)/s}
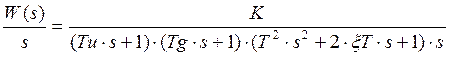
Имеем характеристическое уравнение:
![]()
![]()
Найдём корни характеристического уравнения:
![]()
![]()
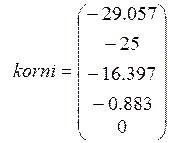
![]()
![]()
![]()
![]()
![]()
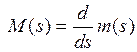
![]()
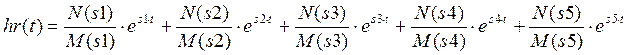
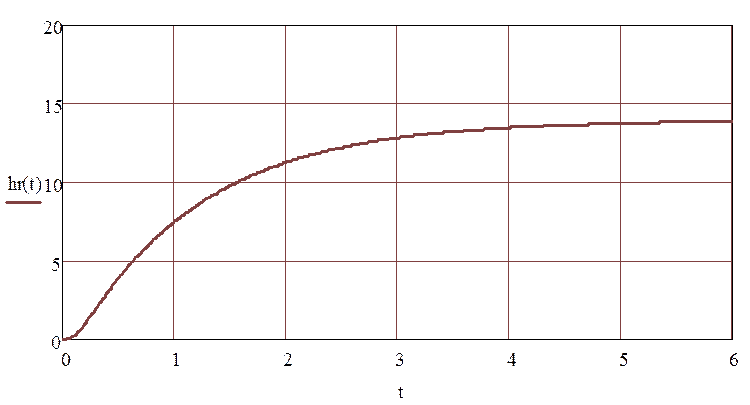
Рисунок 1.5.3 - Переходная характеристика разомкнутой системы с
временем регулирования: ![]()
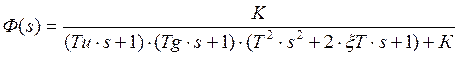 -замкнутая
система
-замкнутая
система
Для нахождения переходной функции используется обратное преобразование Лапласа:
hp(t)=L^(-1){Ф(s)/s}
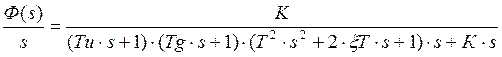
Имеем характеристическое уравнение:
![]()
![]()
Найдём корни характеристического уравнения:
![]()
![]()
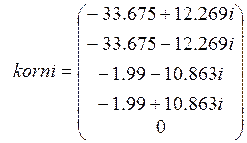
![]()
![]()
![]()
![]()
![]()
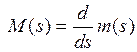
![]()
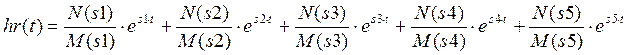
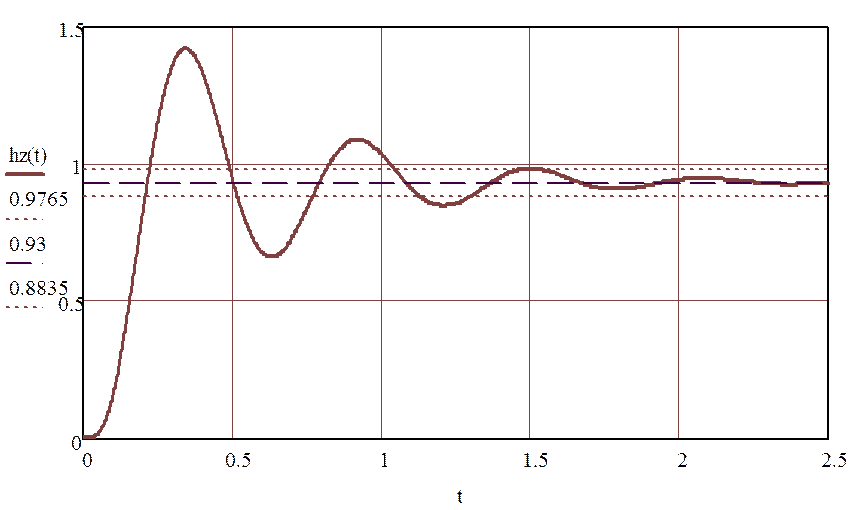
Рисунок 1.5.4 - Переходная характеристика замкнутой системы с
временем
регулирования: ![]()
1.6 Построение электромеханической характеристики в статике для разомкну-той и замкнутой системы. Оценка качества регулирования в статике.
Электромеханическую характеристику строят для замкнутой и разомкнутой сис-тем, для значений напряжения задатчика равных Uzn и 0.5Uzn.
Характеристики строят по трём точкам, при Ic = 0, Ic = 0.5In, Ic = In, где In – номи-нальное значение тока двигателя.
Номинальное значение напряжения двигателя Uzn определяют из условия, что при
напряжении задатчика равном Uzn скорость вращения двигателя в статике при Iс =
0, равна номинальному значению ![]() n
n
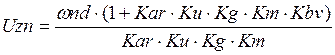 (1.6.1)
(1.6.1)
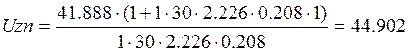
Уравнение электромеханической характеристики для замкнутой системы имеет вид:
![]() (1.6.2)
(1.6.2)
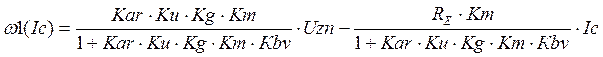 (1.6.3)
(1.6.3)
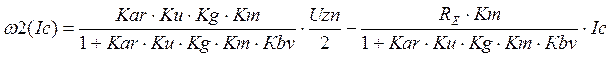 (1.6.4)
(1.6.4)
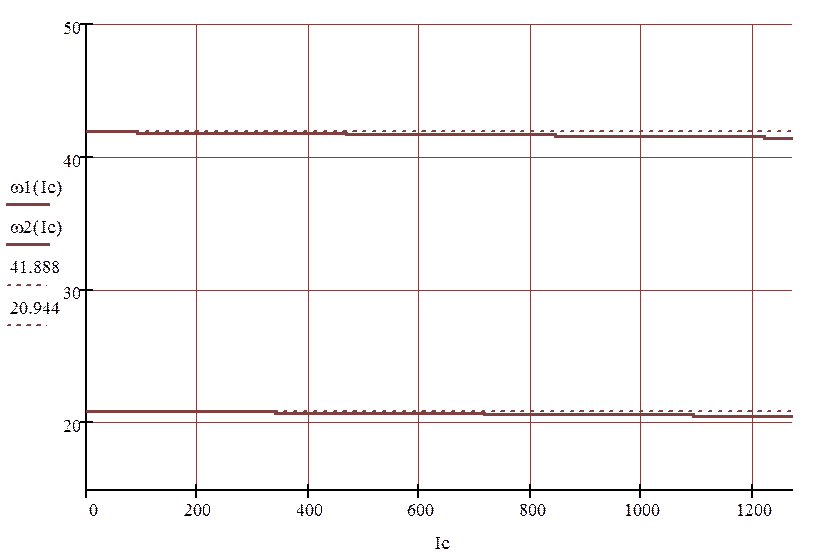
Рисунок 1.6.1 – Электромеханические характеристики для замкнутой системы
По электромеханическим характеристикам, представленным на рисунке 1.6.1, определяют статическую ошибку в замкнутой системе.
![]()
Определить статическую ошибку в замкнутой системе можно также по переда-точной функции по ошибке Feo в статике.
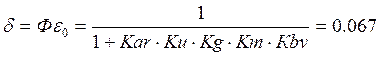
Уравнение электромеханической характеристики для разомкнутой системы имеет вид:
![]() (1.6.5)
(1.6.5)
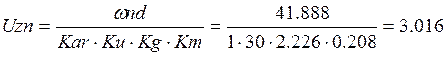 (1.6.6)
(1.6.6)
![]() (1.6.7)
(1.6.7)
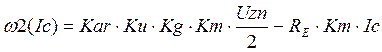 (1.6.8)
(1.6.8)
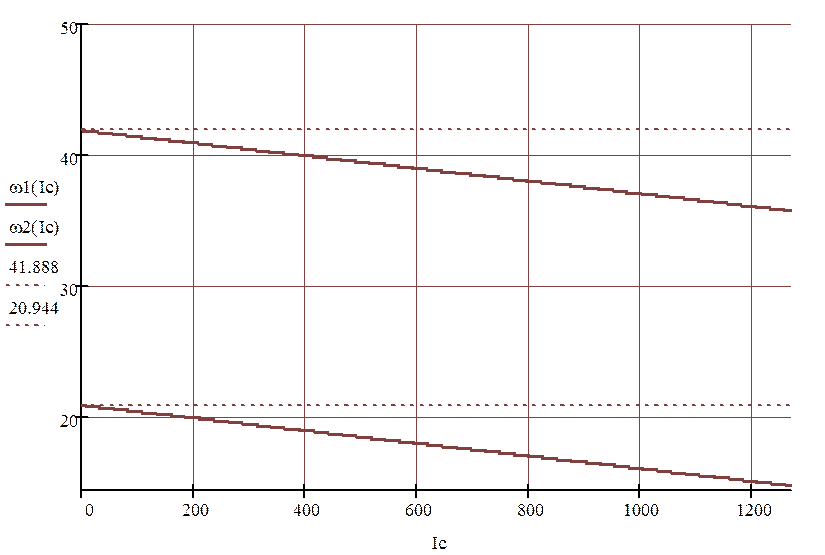
Рисунок 1.6.2 – Электромеханические характеристики для разомкнутой системы
По электромеханическим характеристикам, представленным на рисунке 1.6.2., определяют статическую ошибку в разомкнутой системе.
![]()
2 Оптимизация контура регулирования скорости двигателя по модульному оптимуму.
2.1 Расчёт необходимых настроек регулятора по заданным параметрам регулирования.
Передаточная функция объекта имеет вид:
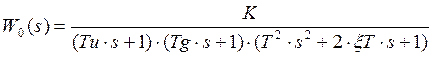
Пусть ![]() тогда
тогда 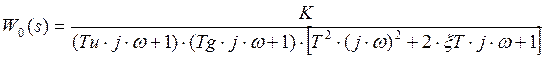
Значит, АЧХ имеет вид: ![]()
ЛАЧХ имеет вид: ![]()
ЛФЧХ имеет вид: 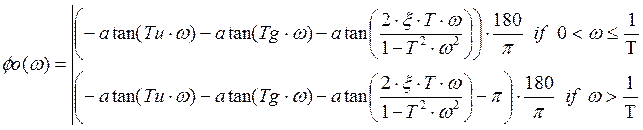
ПИ-регулятор имеет следующую передаточную функцию:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.