Привод механический

горизонтальные составляющие реакций в подшипниках, Н; М_В – изгибающий момент в вертикальной плоскости, Нм; М_Г – изгибающий момент в горизонтальной плоскости, Нм; М_Е – суммарный изгибающий момент, Нм; Т – крутящий момент, Нм.

Рис. 4.2

IIучасток 0 £ х £ 51 мм

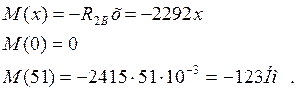
        По этим значениям моментов строим эпюру изгибающих моментов М_В в вертикальной плоскости (рис.4.2).

4) Определим реакции в опорах в горизонтальной плоскости R_1Г и R_2Г. Из условия равновесия вала сумма моментов всех сил относительно какой- либо точки равна нулю.

Относительно точки А

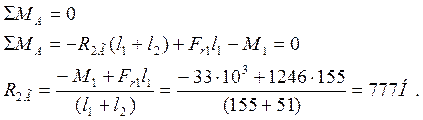
Относительно точки Б

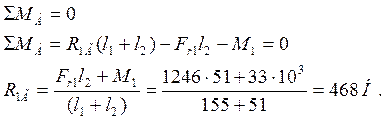
        5) Определим значения изгибающих моментов в горизонтальной плоскости.

Iучасток 0 £ х £ 155 мм

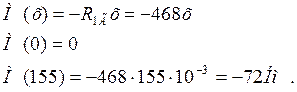
II участок 0£ х £ 51 мм

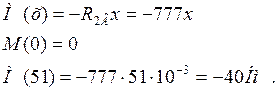
По этим значениям моментов строим эпюру изгибающих моментов М_Г в горизонтальной плоскости (рис.4.2)

        6) Определяем значения суммарных изгибающих моментов.

        Суммарный изгибающий момент в сечении х определяем по формуле

        Вычисляем значения М_Е на границах участков

Iучасток:               

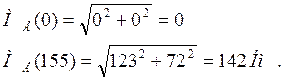
II участок: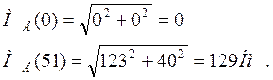                

        По этим значениям моментов строим эпюру суммарных изгибающих

моментов М_Е, действующих на вал (рис. 4.2).

        7) Строим эпюру действующего на вал вращающего момента Т (рис. 4.2).

        8) Определяем полные реакции в подшипниковых опорах 1 и 2

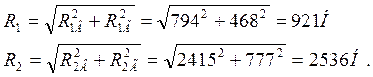
4.3. Расчёт сил и моментов, действующих на промежуточный вал

На рис.4.3 приведена расчётная схема для определения сил и моментов, действующих на промежуточный вал.

Силы F_t2 , F_r2 , F_a2 берём из результатов расчёта быстроходной зубчатой передачи см. п. 2.2.3

;

;

Силы F_t3 , F_r3 , берём из результатов расчёта тихоходной зубчатой передачи см. п. 2.2.3

;

.

        Расстояния принимаем равными l₃ = 77 мм, l₄ = 80 мм, l₅ = 52 мм..

        1) Определим предварительно момент М₂ от силы F_a2

,

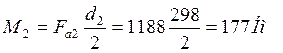где   d₂– делительный диаметр косозубого колеса быстроходной зубчатой передачи, мм; d₂ = 298 мм.

2) Определим реакции в опорах в вертикальной плоскости R_3В и R_4В. Из условия равновесия вала сумма моментов всех сил относительно какой- либо точки равна нулю.

Относительно точки А

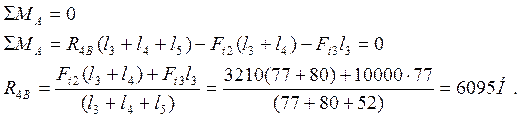
Относительно точки Б

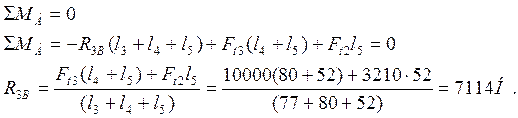
3) Определим значения изгибающих моментов в вертикальной плоскости. Для этого вал условно разделим на три участка (I, II, III).

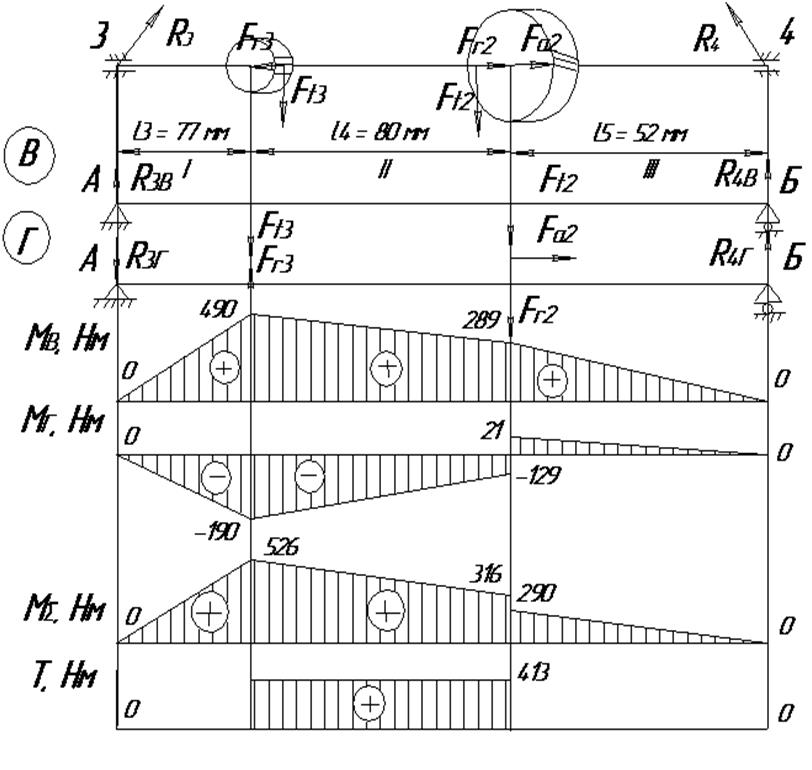
l₃– расстояние между прямозубой шестернёй и подшипником 3, мм; l₄– расстояние между прямозубой шестернёй и косозубым колесом, мм; l₅– расстояние между косозубым колесом и подшипником 4, мм; F_t2– окружная сила, действующая на косозубое колесо, Н; F_r2– радиальная сила, действующая на косозубое колесо, Н; F_a2– осевая сила, действующая на косозубое колесо, Н; F_t3 -окружная сила, действующая на прямозубую шестерню, Н; F_r3– радиальная сила, действующая на прямозубую шестерню, Н; R₃–реакция в подшипнике 3, Н; R₄– реакция в подшипнике 4, Н; R_3B, R_4B– вертикальные составляющие реакций в подшипниках, Н;

R_3Г, R_4Г - горизонтальные составляющие реакций в подшипниках, Н; М_В – изгибающий момент в вертикальной плоскости, Нм; М_Г – изгибающий момент в горизонтальной плоскости, Нм; М_Е – суммарный изгибающий момент, Нм; Т – крутящий момент, Нм.

Рис. 4.3

Iучасток 0 £ х £ 77 мм

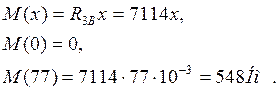
II участок 0£ х £ 80 мм

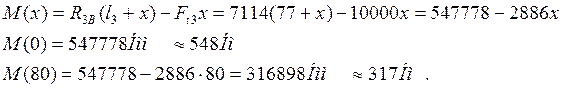
III участок 0£ х £ 52 мм

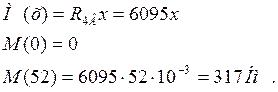
        По этим значениям моментов строим эпюру изгибающих моментов М_В в вертикальной плоскости (рис.4.3).

4) Определим реакции в опорах в горизонтальной плоскости R_3Г и R_4Г. Из условия равновесия вала сумма моментов всех сил относительно какой- либо точки равна нулю.

Относительно точки А

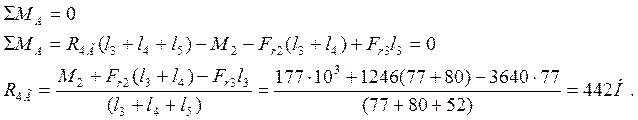
Относительно точки Б

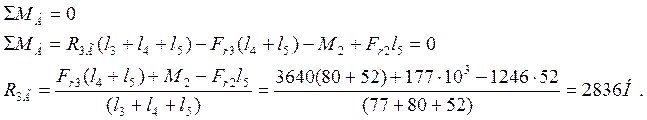
        5) Определим значения изгибающих моментов в горизонтальной плоскости.

I участок 0 £ х £ 77 мм

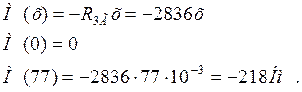
II участок 0£ х £ 80 мм

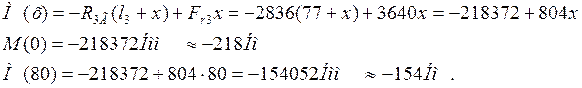
III участок 0£ х £ 52 мм

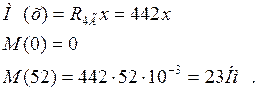
По этим значениям моментов строим эпюру изгибающих моментов М_Г в горизонтальной плоскости (рис.4.3)

        6) Определяем значения суммарных изгибающих моментов.

        Суммарный изгибающий момент в сечении х определяем по формуле

        Вычисляем значения М_Е на границах участков

I участок: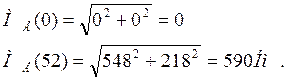                  

II участок: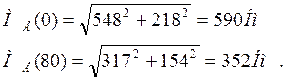                  

III участок: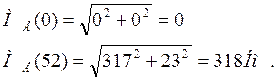                 

        По этим значениям моментов строим эпюру суммарных изгибающих моментов М_Е, действующих на вал (рис. 4.3).

        7) Строим эпюру действующего на вал вращающего момента Т (рис. 4.3).

        8) Определяем полные реакции в подшипниковых опорах 3 и 4

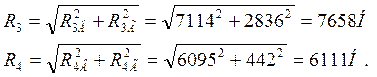
4.4. Расчёт сил и моментов, действующих на тихоходный вал

На рис.4.4 приведена расчётная схема для определения сил и моментов, действующих на тихоходный вал.

Силы F_t4 , F_r4 берём из результатов расчёта тихоходной зубчатой передачи см. п. 2.2.3

;

;

        Расстояния принимаем равными l₆ = 81 мм, l₇ = 136 мм, l₈ = 126 мм..

        1) Определим предварительно момент М_М , возникающий при работе компенсирующей муфты

принимаем М_М = 180 Нм.

        Сила F_М , возникающая при работе компенсирующей муфты

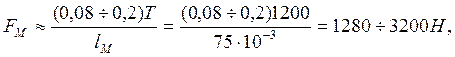
где   l_M– расстояние между зубчатыми венцами муфты, мм; l_М = 75 мм.

Принимаем F_M = 3200 Н.

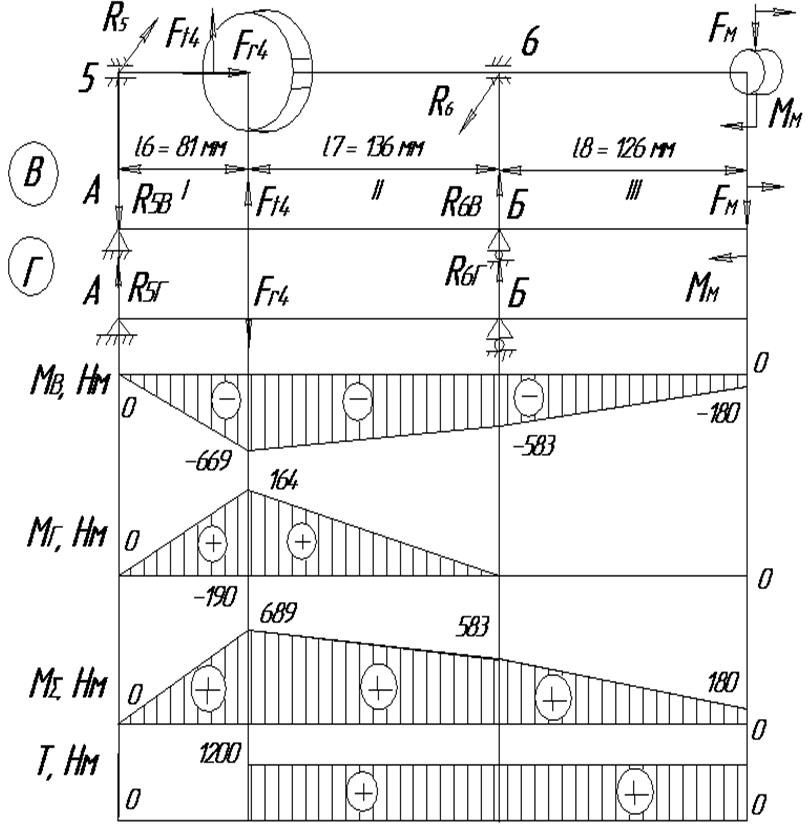
l₆– расстояние между прямозубым колесом и подшипником 5, мм; l₇– расстояние между прямозубым колесом и подшипником 6, мм; l₈– расстояние между подшипником 6 и муфтой, мм; F_t4– окружная сила, действующая на прямозубое колесо, Н; F_r4– радиальная сила, действующая на прямозубое колесо, Н; R₅–реакция в подшипнике 5, Н; R₆– реакция в подшипнике 6, Н; R_5B, R_6B– вертикальные составляющие реакций в подшипниках, Н; R_5Г, R_6Г - горизонтальные составляющие реакций в подшипниках, Н; F_M– сила, возникающая при работе компенсирующей муфты, Н; М_М – момент, возникающий при работе компенсирующей муфты, Нм; М_В – изгибающий момент в вертикальной плоскости, Нм; М_Г – изгибающий момент в горизонтальной плоскости, Нм; М_Е – суммарный изгибающий момент, Нм; Т – крутящий момент, Нм.

Рис. 4.4

2) Определим реакции в опорах в вертикальной плоскости R_5В и R_6В. Из условия равновесия вала сумма моментов всех сил относительно какой- либо точки равна нулю.

Относительно точки А

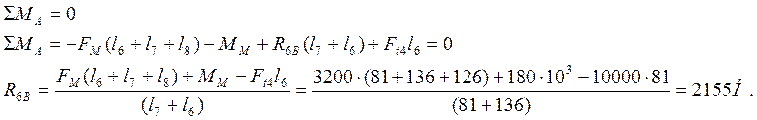
Относительно точки Б

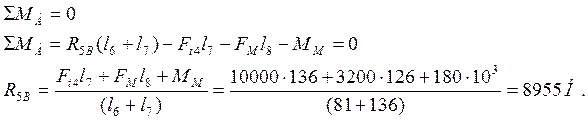
3) Определим значения изгибающих моментов в вертикальной плоскости. Для этого вал условно разделим на три участка (I, II, III).

I участок 0£ х £ 81 мм

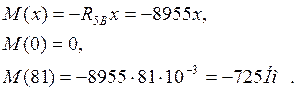
II участок 0£ х £ 136 мм

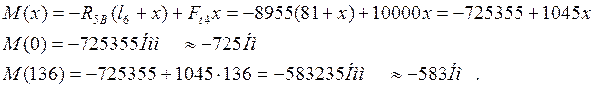
III участок 0£ х £ 126 мм

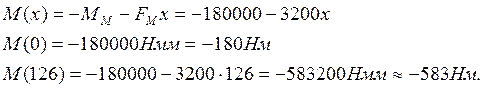
        По этим значениям моментов строим эпюру изгибающих моментов М_В в вертикальной плоскости (рис.4.4).

4) Определим реакции в опорах в горизонтальной плоскости R_5Г и R_6Г. Из условия равновесия вала сумма моментов всех сил относительно какой- либо точки равна нулю.

Относительно точки А

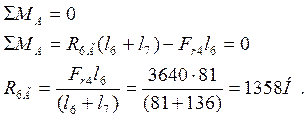
Относительно точки Б

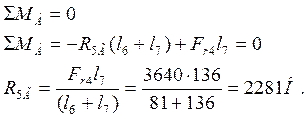
        5) Определим значения изгибающих моментов в горизонтальной плоскости.

I участок 0 £ х £ 81 мм

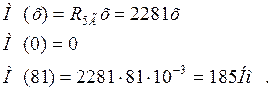
II участок 0£ х £ 136 мм

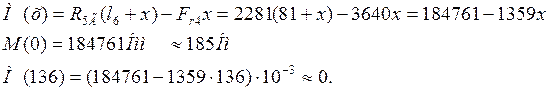
III участок 0£ х £ 126 мм

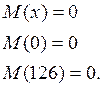
По этим значениям моментов строим эпюру изгибающих моментов М_Г в горизонтальной плоскости (рис.4.4)

        6) Определяем значения суммарных изгибающих моментов.

        Суммарный изгибающий момент в сечении х определяем по формуле

        Вычисляем значения М_Е на границах участков

I участок: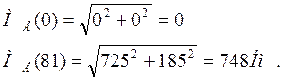                 

II участок: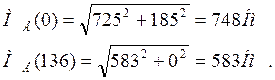                  

III участок: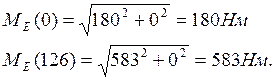                

        По этим значениям моментов строим эпюру суммарных изгибающих моментов М_Е, действующих на вал (рис. 4.4).

        7) Строим эпюру действующего на вал вращающего момента Т (рис. 4.4).

        8) Определяем полные реакции в подшипниковых опорах 5 и 6

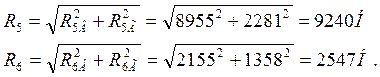
5. Проектирование подшипниковых узлов

        Задачами раздела являются:

-  выбор подшипников качения для всех валов редуктора;

-  описание основ методики проверочного расчёта подшипников качения;

-  заполнение бланков исходных данных для расчёта на ЭВМ;

-  анализ результатов расчёта.

5.1. Выбор подшипников качения

По конструктивным соображениям выбираем следующие подшипники:

для быстроходного вала:

- Подшипник 46207 ГОСТ 831-75, 2 шт.

для промежуточного вала:

- Подшипник 46209 ГОСТ 831-75, 2 шт.

для тихоходного вала:

- Подшипник 213 ГОСТ 8338-75, 2 шт.

        5.2. Основы методики расчёта

        Методику расчёта рассмотрим на примере радиально-упорных подшипников.

    Исходные данные:

1) Вал установлен на двух подшипниках шариковых радиально- упорных лёгкой серии 46207 (ГОСТ 831-75). Схема приведена на рис. 5.1

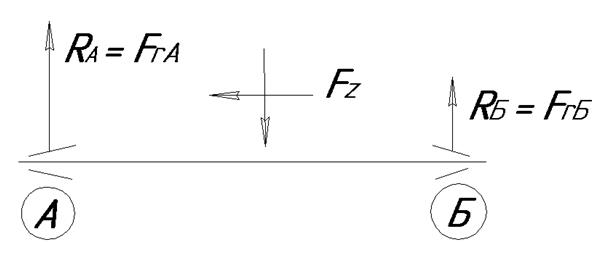
Рис. 5.1

2) Радиальные реакции

;

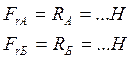значения этих сил приведены в разделе 4.

3) Внешняя осевая сила F_Z

;

значение силы приведено в п.2.2.3.

4) Частота вращения n

n = … об/мин;

значение см. раздел 1.

        5) Динамическая грузоподъёмность С

С = … Н;

        значение величины берётся из справочника (9).

        6) Требуемый ресурс работы подшипника

[L_h] = ... часов;

        значение этой величины берётся из технического задания.

Условие работоспособности подшипников

,

где   L_h– расчётный ресурс, часы;

        [L_h] – требуемый ресурс, часы.

        Расчётный ресурс определяется из выражения

,

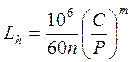где   Р – приведённая нагрузка, Н;

m– коэффициент; для шариковых подшипников m = 3.

        Приведённую нагрузку определяют из выражения

,

где   Х – коэффициент, учитывающий радиальную нагрузку;

Y– коэффициент, учитывающий осевую нагрузку;

        к_б – коэффициент безопасности;

        к_т – температурный коэффициент, учитывает температурные условия, в которых работает подшипник;

V– коэффициент вращения;.

        Расчётная схема нагружения подшипника приведена на рис. 5.2

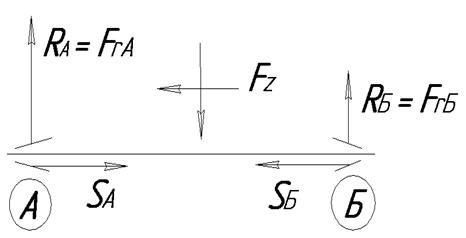
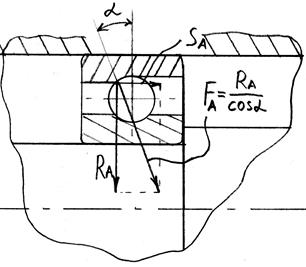
А и Б – подшипники; F_rA, F_rБ– радиальные составляющие нагрузки подшипников, Н;S_A, S_Б– осевые составляющие нагрузки

подшипников, вызванные действием радиальных

нагрузок, Н; F_Z– внешняя осевая сила, Н.

Рис. 5.2

Определяют осевые составляющие нагрузки подшипников S_A и S_Б

 

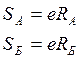
        Определяют полные осевые нагрузки F_aA, F_аБ действующие на подшипники.

        Для этого рассмотривают условия

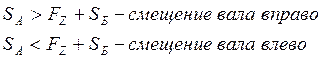
  Далее определяют коэффициенты X и Y, Для этого рассматриваются условия:

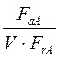 > е

или

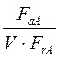 < е

         По справочнику для подшипника в опоре А определяют коэффициенты:

X_А = …

Y_А = …

Теперь определяют коэффициенты X и Y для подшипника Б. Для этого рассматривают условия:

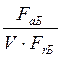 > е

или

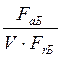 < е

По справочнику для подшипника в опоре Б:

X_Б = …

Y_Б = …

        Определяют приведённую нагрузку подшипников

Н

Н,

        Определяют ресурс наиболее нагруженного подшипника (предположим это подшипник А)

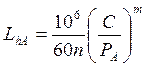
Проверяют условие работоспособности подшипников

L_h³ [L_h].

Условие работоспособности подшипников выполняется, если

L_h = …> [L_h] = …

        5.3. Исходные данные для расчёта на ЭВМ

        Исходные данные для расчёта подшипников редуктора представлены в табл.5.1.

Таблица 5.1

Исходные данные для расчёта подшипников качения

Вал	Условное обозначение подшипников	Ресурс	Режим нагружения	Коэффициент безопасности	Частота вращения вала	Схема нагружения и силы
		L			n
		часы			об/мин
Б	46207	5500	10	1,3	578	R’ = 877Н R’’ = 2406 Н А = 1093 Н
Пр	46209				120	R’ = 6829Н R’’ = 5575 Н А = 1093 Н
Т	213				40	R’ = 8499Н R’’ = 2841 Н

Во всех случаях относительно нагрузки вращается внутреннее кольцо подшипника.

        5.4. Результаты расчёта

 

        Из результатов расчёта видим, что условие работоспособности выполняется для всех подшипников на каждом валу.

6. Проверочный расчёт шпоночных соединений

        Задачей раздела является оценка прочности шпоночных соединений. Оценку будем проводить из условий на смятие и на срез шпонки.

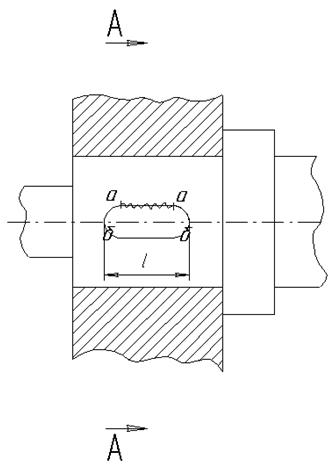
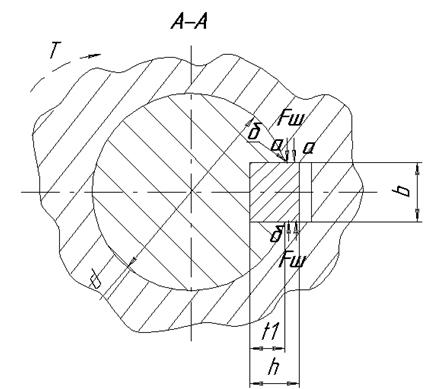
Расчётная схема для проверочного расчёта приведена на рис. 6.1

а–а – опасное сечение на смятие шпонки; б-б – опасное сечение на срез шпонки;l– длина шпонки, мм; Т – вращающий момент, Нм; F_ш– силы, действующие на шпонку со стороны колеса, Н; b– ширина шпонки, мм;

h– высота шпонки, мм;t₁– глубина паза вала, мм;

d– диаметр вала, мм.

Рис. 6.1

        Выполним проверочный расчёт на смятие узкой грани шпонки в сечении а-а (рис.6.1). Условие отсутствия смятия шпонки под косозубым колесом на промежуточном валу

,

где   s_см– действующее напряжение смятия, МПа;

        [s_см] – допустимое напряжение смятия, МПа;

,

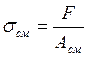где   F– сила, действующая на шпонку со стороны косозубого колеса, Н;

        А_см – площадь опасного сечения на смятие, мм²;

,

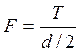где   Т – вращающий момент на валу, Нм; Т = 413 Нм;

d– диаметр вала, мм; d = 50 мм;

,

где   h– высота шпонки, мм; h = 10 мм;

t₁– глубина паза вала, мм; t₁ = 6 мм;

l– длина шпонки, мм; l = 45 мм;

b– ширина шпонки, мм; b = 16 мм.

Таким образом,

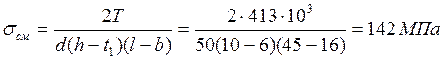
        Принимаем [s_см] = 160 МПа.

        Проверяем условие смятия

.

        Условие выполнено.

        Выполним проверочный расчёт на отсутствие среза шпонки в сечении б-б (рис. 6.1), под косозубым колесом на промежуточном валу

,

где   t_ср– действующее напряжение среза, МПа;

        [t_ср] – допустимое напряжение среза, МПа;

,

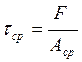где   А_ср – площадь опасного сечения среза, мм²;

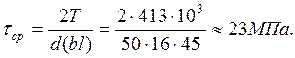
        Допустимое напряжение среза определяем из условия

        Проверяем условие среза

        Условие выполнено.

        Выполним проверочный расчёт на смятие узкой грани шпонки в сечении а-а (рис.6.1), для шпонки под прямозубой шестернёй на промежуточном валу

,

где   s_см– действующее напряжение смятия, МПа;

        [s_см] – допустимое напряжение смятия, МПа;

,

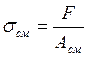где   F– сила, действующая на шпонку со стороны шестерни, Н;

        А_см – площадь опасного сечения на смятие, мм²;

,

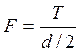где   Т – вращающий момент на валу, Нм; Т = 413 Нм;

d– диаметр вала, мм; d = 50 мм;

,

где   h– высота шпонки, мм; h = 10 мм;

t₁– глубина паза вала, мм; t₁ = 6 мм;

l– длина шпонки, мм; l = 85 мм;

b– ширина шпонки, мм; b = 16 мм.

Таким образом,

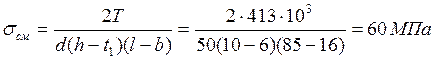
        Проверяем условие смятия

.

        Условие выполнено.

        Выполним проверочный расчёт на отсутствие среза шпонки в сечении б-б (рис. 6.1), под прямозубой шестернёй на промежуточном валу

,

,

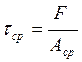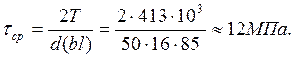
        Допустимое напряжение среза определяем из условия

        Проверяем условие среза

        Условие выполнено.

Выполним проверочный расчёт на смятие узкой грани шпонки в сечении а-а (рис.6.1), для шпонки под прямозубым колесом на тихоходном валу

,

,

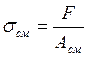где   F– сила, действующая на шпонку со стороны прямозубого колеса, Н;

        А_см – площадь опасного сечения на смятие, мм²;

,

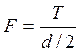где   Т – вращающий момент на валу, Нм; Т = 1200 Нм;

d– диаметр вала, мм; d = 70 мм;

,

где   h– высота шпонки, мм; h = 12 мм;

t₁– глубина паза вала, мм; t₁ = 7,5 мм;

l– длина шпонки, мм; l = 85 мм;

b– ширина шпонки, мм; b = 20 мм.

Таким образом,

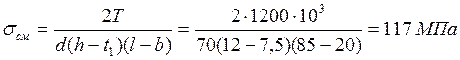
        Проверяем условие смятия

.

        Условие выполнено.

        Выполним проверочный расчёт на отсутствие среза шпонки в сечении б-б (рис. 6.1), под прямозубым колесом на тихоходном валу

,

,

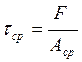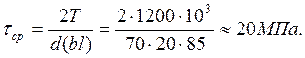
        Допустимое напряжение среза определяем из условия

        Проверяем условие среза

        Условие выполнено.

        Выполним проверочный расчёт на смятие узкой грани шпонки в сечении а-а (рис.6.1), для шпонки под муфтой

,

,

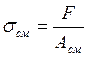где   F– сила, действующая на шпонку со стороны муфты, Н;

,

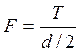где   Т – вращающий момент на валу, Нм; Т = 1200 Нм;

d– диаметр вала, мм; d = 56 мм;

,

где   h– высота шпонки, мм; h = 12 мм;

t₁– глубина паза вала, мм; t₁ = 7,5 мм;

l– длина шпонки, мм; l = 95 мм;

b– ширина шпонки, мм; b = 20 мм.

Таким образом,

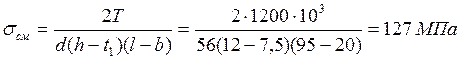
        Проверяем условие смятия

.

        Условие выполнено.

        Выполним проверочный расчёт на отсутствие среза шпонки в сечении б-б (рис. 6.1), под шестернёй

,

,

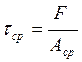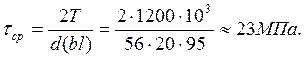
        Допустимое напряжение среза определяем из условия

        Проверяем условие среза

        Условие выполнено.

Результаты расчёта сведём в табл. 6.1

Таблица 6.1

Результаты расчёта

Соединение	bxhxl, мм	scм, МПа	[scм], МПа	tср, МПа	[tср], МПа
Под косозубым колесом	16х10х45	142	160	23	96
Под прямозубой шестернёй	16х10х85	60		12
Под прямозубым колесом	20х12х85	117		20
Под муфтой	20х12х95	127		23

7. Проверочный расчёт валов в опасных сечениях

  Будем проверять опасные сечения и сечения, в которых имеется концентрация напряжений. При проверке определяется расчетный коэффициент запаса прочности S и сопоставляется с допускаемым [S].

Ограничимся проверкой промежуточного вала, так как на нём установлено зубчатое колесо и шестерня. Исходными данными для расчётов являются: конструкция вала и эпюры действующих на вал изгибающих и вращающего моментов, представленные