Установки с ДВС. Выбор типа двигателя., страница 3

При

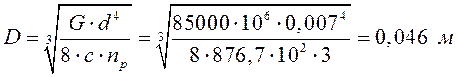
Сила, действующая на одну пружину, равна:

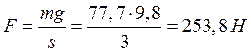
Статическая деформация пружины равна:

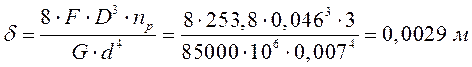
Шаг пружины равен:

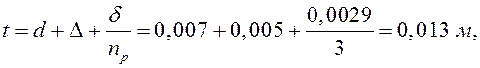
где Δ=5мм - гарантированный зазор между витками пружины.

Высота пружины:

где - суммарная толщина нерабочих витков пружины.

Проведем проверку касательных напряжений при кручении. Для пружиной стали 50ХФА допустимое касательное напряжение 

 

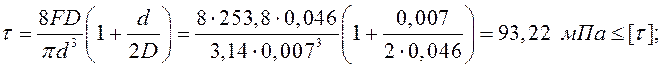
Эскиз пружины представлен на рисунке 4.

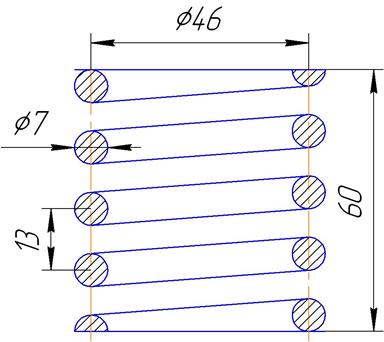
Рисунок 4 Эскиз пружины

Расчет системы охлаждения

Расчет водяного радиатора

Определим количество теплоты, введенной в цилиндры с топливом:

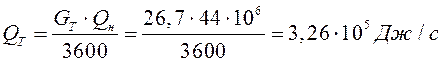
где G_T – расход топлива на расчетном режиме, кг/ч;

Q_н – низшая теплотворная способность топлива,  Дж/кг.

Найдем количество теплоты, отдаваемой в охлаждаемую жидкость:

Вычислим циркуляционный расход охлаждающей жидкости:

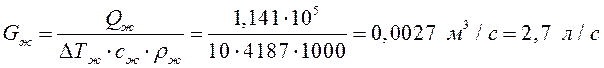
где  – средняя плотность воды.

Рассчитаем поверхность охлаждения радиатора:

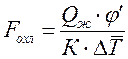
где  - коэффициент запаса, учитывающий ухудшение теплообмена из-за загрязнения решетки;

 - коэффициент теплопередачи радиатора;             , где - средняя температура охлаждающей жидкости;

- средняя температура воздуха, проходящего через радиатор;

- температурный перепад воздуха в решетке радиатора.

Расчет вентилятора

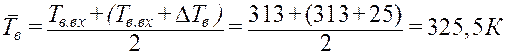
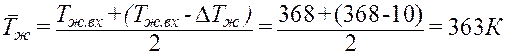
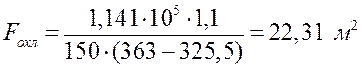
Производительность вентилятора (м³/с):

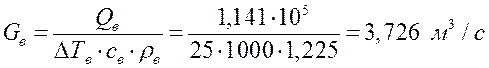, где  - количество теплоты, отводимое от радиатора охлаждающим воздухом, Дж/с;

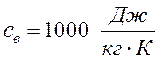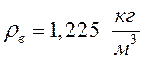 - удельная теплоемкость воздуха;

 - плотность воздуха.

Диаметр вентилятора:

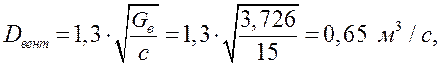
где - скорость протекания воздуха через проточную часть вентилятора.

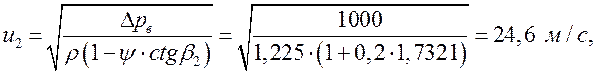
где ; ;  - сопротивление воздушного тракта.

Рассчитаем угловую частоту:

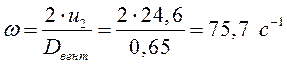
Рассчитаем частоту вращения вентилятора:

Расчет водяного насоса

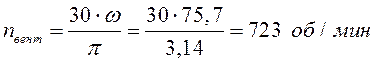
Расчетная величина подачи насоса (л/с) равна:

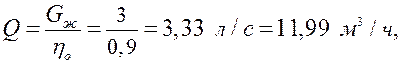
где  - объемный КПД насоса.

Потери напора:

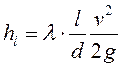
-  Для линии всасывания: l=3,25 м – длина трубопровода; λ=0,02 – коэффициент трения в трубе.

Диаметр трубопровода на линии всасывания:

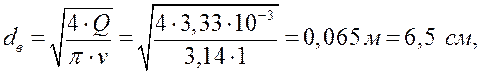
Где - средняя скорость жидкости во всасывающем трубопроводе.

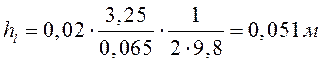
-  Для линии нагнетания: l=3,25 м – длина трубопровода; λ=0,02 – коэффициент трения в трубе.

Диаметр трубопровода на линии нагнетания:

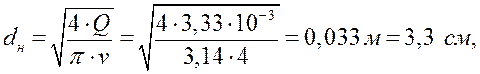
Где - средняя скорость жидкости в нагнетающем трубопроводе.

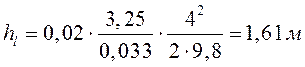
Потери напора в клапане:

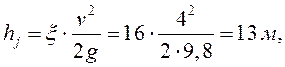
где - коэффициент местных потерь насоса.

Полные потери насоса:

Вывод: необходим насос с подачей  и напором

Марка насоса: К12/15.

3.  Внешний тепловой баланс и эксергетический кпд двигателя.

Теплота, выделяющаяся при сгорании топлива в цилиндрах двигателя, не может быть полностью преобразована в полезную механическую работу. В термодинамическом цикле эффективность превращения теплоты в работу оценивается термическим кпд , который всегда остаётся меньше единицы вследствие передачи части теплоты холодному источнику. В реальном двигателе потери теплоты возрастают из-за трения, теплообмена, неполноты сгорания и других причин. В связи с этим эффективный кпд цикла имеет меньшее значение по сравнению с величиной .

Распределение тепловой энергии топлива, сгорающего в двигателе, наглядно иллюстрируется составляющими внешнего теплового баланса, которые определяются при установившемся тепловом состоянии двигателя в процессе его испытаний. Приближенно составляющие теплового баланса можно найти аналитически по данным теплового расчёта двигателя.

Тепловой баланс позволяет определить теплоту, превращённую в полезную эффективную работу, т.е. установить степень достигнутого совершенства использования теплоты и наметить пути уменьшения имевшихся потерь. Знание отдельных составляющих теплового баланса позволяет судить о теплонапряжённости деталей двигателя, рассчитать схему охлаждения, выяснить возможность использования теплоты отработавших газов и т.д.

В общем виде внешний тепловой баланс двигателя может быть представлен в виде следующих составляющих:

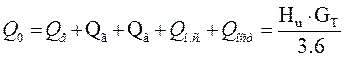, где Q₀ – общее количество теплоты, введенной в двигатель с топливом.

Q_e – теплота, эквивалентная эффективной работе двигателя за 1с;

Q_г – теплота, потерянная с отработавшими газами;

Q_в – теплота, передаваемая окружающей среде;

Q_н.с. – теплота, потерянная из-за химической неполноты сгорания топлива;