Основы корреляционного и регрессионного анализа

2. ОСНОВЫ КОРРЕЛЯЦИОННОГО И РЕГРЕССИОННОГО АНАЛИЗА

2.1. ВВЕДЕНИЕ

Во многих технических, экономических, организационных задачах требуется установить и оценить зависимость изучаемой случайной величины Y от одной или нескольких других величин X. Например, в ситуациях, когда необходимо оценить как влияет:

1) количество внесенных удобрений на снимаемый урожай;

2) величина затрат компании на рекламу своего товара на объемы продаж этого товара;

3) изменение цены товара на объем его продаж;

4) величина доходов населения на величину их сбережений.

Зависимость между значениями параметров X и Y может быть:

n функциональной;

n статистической;

n корреляционной.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Параметр Y связан с параметром X функциональной зависимостью в том случае, когда конкретному значению  соответствует одно и только одно значение  [My]. Например, если принять, что X - это градусы по шкале Цельсия, а Y - градусы по шкале Фаренгейта, то между этими параметрами существует функциональная зависимость

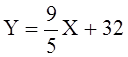
и наоборот

.

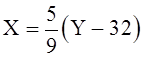Функциональность связи определяется тем, что для конкретной температуры по Цельсию существует одна и только одна температура по Фаренгейту.

Строгая функциональная зависимость реализуется редко, т.к. часто оба параметра или один из них подвержены еще действию разнообразных случайных факторов, например, объем продаж товара не определяется жестко его ценой. На него могут влиять такие случайные факторы, как погода, сезон, эффект ажиотажного спроса, массовая невыплата или выплата зарплаты. Если среди этих случайных факторов имеются общие для обоих параметров (т.е. воздействующие и на X и на Y), то зависимость называется статистической например, !!!..

Таким образом, статистической называют зависимость, при которой изменение одной из величин влечет изменение распределение другой. Например, пусть при цене на лимоны в 7 руб. семья со средним достатком покупает в месяц от 10 до 15 лимонов, при цене в 13 руб. - от 5 до 10 шт., а при цене в 25 руб. - 1-3 шт. Т.е. изменение цены X изменяет возможное количество покупаемых цитрусовых Y.

Статистическую зависимость называют корреляционной, если при изменении одной из величин изменяется среднее значение другой. Например, с одинаковых по площади участков земли при равных количествах внесенных удобрений X снимают различный урожай Y, т.е. Y не является функцией от X. Это объясняется влиянием случайных факторов (осадки, температура воздуха, плодородие почвы и др.). Но как показывает опыт, средний урожай является функцией от количества удобрений, т.е. Y связан с X корреляционной зависимостью.

Законом распределения дискретной случайной величины (СВ) называют соответствие между возможными ее значениями и их вероятностями.

Дискретная СВ - это СВ, которая принимает отдельные изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Корреляционный и регрессионный анализ - это смежные разделы математической статистики, предназначенные для разработки и анализа математических уравнений или моделей статистических связей между параметрами.

2.2. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

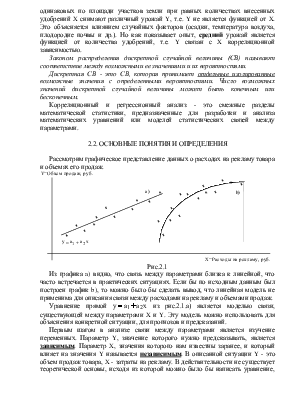
Рассмотрим графическое представление данных о расходах на рекламу товара и объемах его продаж.

Рис.2.1

Из графика a) видно, что связь между параметрами близка к линейной, что часто встречается в практических ситуациях. Если бы по исходным данным был построен график b), то можно было бы сделать вывод, что линейная модель не применима для описания связи между расходами на рекламу и объемами продаж.

Уравнение прямой  из рис.2.1.а) является моделью связи, существующей между параметрами X и Y. Эту модель можно использовать для объяснения конкретной ситуации, для прогнозов и предсказаний.

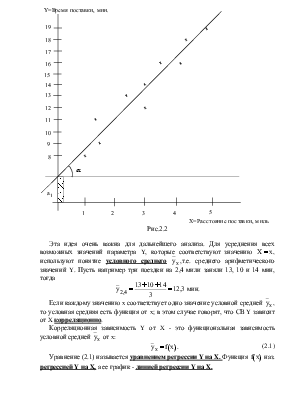
Первым шагом в анализе связи между параметрами является изучение переменных. Параметр Y, значение которого нужно предсказывать, является зависимым. Параметр X, значения которого нам известны заранее, и который влияет на значения Y называется независимым. В описанной ситуации Y - это объем продаж товара, X - затраты на рекламу. В действительности не существует теоретической основы, исходя из которой можно было бы написать уравнение, которое бы точно показало связь продаж с расходами на рекламу. Имеется ряд факторов, неразрывно связанных между собой, такие как цена товара, цена товара-конкурента, сезон, погодные условия. Тем не менее, если предположить, что в конкретном случае, расходы на рекламу являются главным фактором, определяющим продажу, то знание этой связи было очень полезным для оценки объема продаж и соответствующего планирования финансовой политики компании.

Другой пример, пусть, например, фермер хочет предсказывать вес кур, зная их возраст. В этом случае Y - это вес курицы, X - ее возраст. Конечно, вес курицы определяется не только возрастом, но и породой, способом кормления, погодными условиями и т.д. Но если предположить, что на конкретной ферме все факторы, кроме возраста, примерно одинаковы, то можно попытаться предсказывать вес курицы только на основании ее возраста.

ПРИМЕР