Основы корреляционного и регрессионного анализа, страница 2

Пусть некоторая фирма занимается поставками различных грузов на короткие расстояния внутри города. Перед менеджером стоит задача оценить стоимость таких услуг, зависящую от затрачиваемого на поставку времени. К факторам, влияющим на время поставки, относятся: пройденное расстояние, пробки на дорогах, время суток, дорожные работы, погода, квалификация водителя, вид транспорта. Для упрощения задачи будем рассматривать связь между расстоянием (независимый параметр X) и затраченным временем (зависимый параметр Y). В качестве исходных данных для анализа будем использовать выборочные данные о десяти поставках.

Табл.2.1

Построенные точки не находятся точно на линии, что обусловлено описанными выше факторами. Но эти точки собраны вокруг прямой линии, поэтому можно предположить линейную связь между параметрами.

Важным уточнением наших рассуждений является то, что для любого конкретного расстояния существует распределение возможного времени поставок, т.е. не одно, а несколько значений y, например для ,  и . Если мы рассмотрим большее количество поставок, то каждому значению x будет соответствовать большее количество значений y.

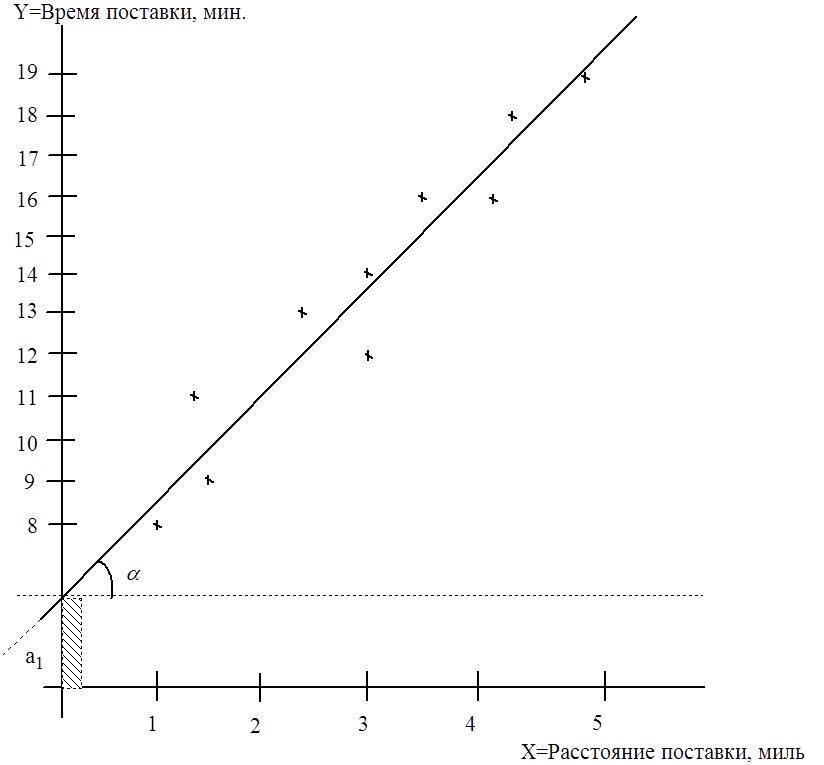
Рис.2.2

Эта идея очень важна для дальнейшего анализа. Для усреднения всех возможных значений параметра Y, которые соответствуют значению , используют понятие условного среднего ,т.е. среднего арифметического значений Y. Пусть например три поездки на 2,4 мили заняли 13, 10 и 14 мин, тогда

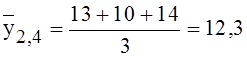 мин.

Если каждому значению x соответствует одно значение условной средней , то условная средняя есть функция от x; в этом случае говорят, что СВ Y зависит от X корреляционно.

Корреляционная зависимость Y от X - это функциональная зависимость условной средней  от x:

Уравнение (2.1) называется уравнением регрессии Y на X. Функция  наз. регрессией Y на X, а ее график - линией регрессии Y на X.

Точно также вводятся понятия условной средней  и корреляционной зависимости X от Y.

В регрессионном и корреляционном анализе существует две основные задачи.

1) Установить форму корреляционной связи, т.е. вид функции регрессии (линейная, квадратичная, показательная и т.д.). Наиболее часто функции регрессии оказываются линейными.

2) Оценить тесноту (силу) корреляционной связи. Теснота корреляционной зависимости Y от X оценивается по величине рассеяния значений Y вокруг условного среднего . Большое рассеяние говорит о слабой зависимости Y от X, либо об ее отсутствии. И наоборот, Малое рассеяние указывает наличие достаточно сильной зависимости [Гмурман].

Искомое уравнение линейной регрессии Y на X имеет вид

где  - коэффициент регрессии. Значение  определяет точку пересечения линии регрессии с осью OY, значение  - это угловой коэффициент прямой (2.2), т.е. , где  - угол между прямой и осью OX.

При этом параметры  и  должны быть подобраны таким образом, чтобы точки, построенные по исходным данным , лежали как можно ближе к прямой (2.2). Чтобы выполнить это требование, необходимо учитывать разность наблюдаемого значения  и теоретически вычисленного по уравнению (2.2)

, которая называется отклонением, ошибкой, остатком. Тогда линейное уравнение, которое наилучшим образом аппроксимирует данные, должно определять наименьшее суммарное значение этих отклонений. Для удобства расчетов и для устранения компенсации положительных отклонений отрицательных используют не сами отклонения, а их квадраты. Метод нахождения уравнений регрессии (не только линейной), который основан на минимизации суммы квадратов отклонений

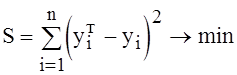, где n - количество пар исходных данных, наз. методом наименьших квадратов.

2.3. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

2.3.1. Линейная регрессия

Т.к. в случае линейной регрессии каждое отклонение зависит от параметров  и , то сумма квадратов отклонений является функцией от этих параметров