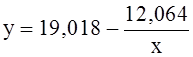Основы корреляционного и регрессионного анализа, страница 4

.

Для приведения модели (2.7) к линейному виду необходимо провести логарифмирование

;

;

.

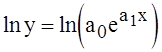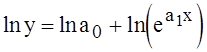Введем переменные  и , тогда

, отсюда следует, что можно применять формулы (2.4), (2.5), в которых вместо значений  надо использовать . При этом мы получим численные значения коэффициентов  и , от которых надо перейти к  и , которые использованы в модели (2.7). Из определения логарифма, а также согласно введенным обозначениям

.

(2.8)

=;

=.

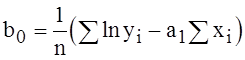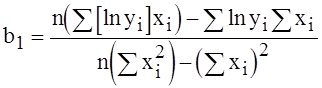x	y
3,5	16	2,773		12,25
2,4	13	2,565		5,76
4,9	19	2,944		24,01
4,2	18	2,890		17,64
3,0	12	2,485		9,00
1,3	11	2,398		1,69
1,0	8	2,079		1,00
3,0	14	2,639		9,00
1,5	9	2,197		2,25
4,1	16	2,773		16,81
28,9	136			99,41

Для примера о времени поставок модель регрессии (2.7) имеет следующий вид

.

График отклонений имеет вид.

Сравнив суммы квадратов отклонений моделей (2.2), (2.6) и (2.7) делаем вывод, что линейная модель наиболее точно описывает исходные данные примера, т.к. имеет min сумму. Кроме того, ...

2.5. ОЦЕНКА ТЕСНОТЫ ЛИНЕЙНОЙ СВЯЗИ

Подбор вида функции регрессии на основе графика (как в рассмотренном примере о поставках) может быть обманчивым, поскольку распределение исходных точек на графике, а значит и общий вид графика, зависит от выбора масштаба. Поэтому необходимо объективное измерение тесноты линейной связи [Эддоус].

(Мат. ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений СВ .

Дисперсия - это числовая характеристика СВ, которая показывает, как рассеяны возможные значения СВ вокруг ее математического ожидания. Дисперсия - это мат. ожидание квадрата отклонения СВ от ее математического ожидания, ).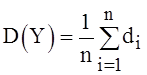

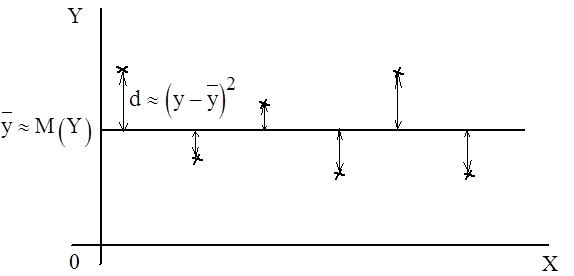
Рассмотрим на графике структуру дисперсии зависимой переменной Y.

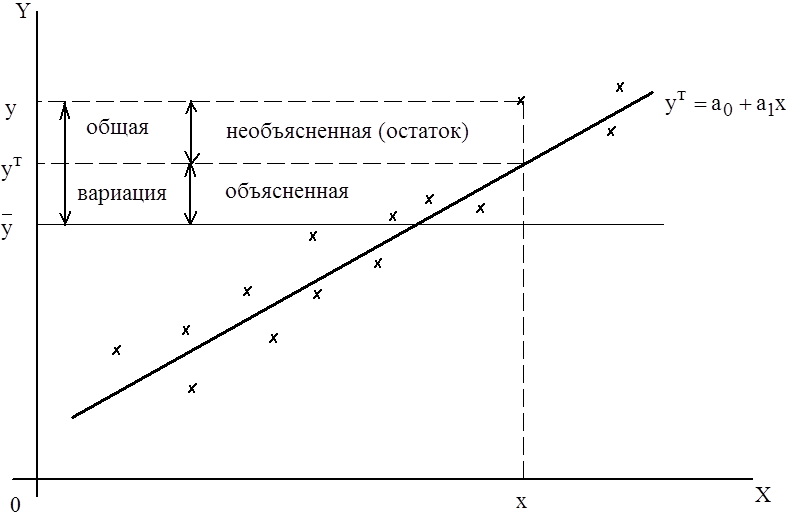
Линейная связь только частично объясняет разброс значений y. Необъясненная часть является остатком e. Если бы связь между x и y была абсолютно линейной, то все e были бы равны нулю. По мере того, как сила линейной связи уменьшается, остаток увеличивается. Общая вариация значений y равна

.

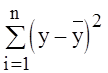Общее изменение y с учетом линейной связи, т.е. объясненная вариация равна

.

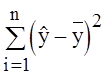Тогда вариация, которая не объясняется линейной связью, поскольку возникает из-за других факторов, не включенных в линейную модель равна

.

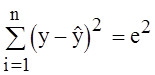Чем теснее линейная связь, тем ближе величина объясненной вариации к величине общей вариации. Поэтому используется отношение этих вариаций, называемое коэффициентом детерминации [Эддоус ]

.

(2.8)

Коэффициент детерминации показывает величину дисперсии Y, которая объясняется независимой переменной X. Он часто выражается в процентах и в случае линейной связи между параметрами равен  или 100%. Если линейная связь отсутствует, то .

Большую информацию о связи между параметрами можно получить при использовании коэффициента корреляции Пирсона (выборочного коэффициента корреляции)

или .

(2.9) (2.10)

(Дополнительное задание: провести алгебраические преобразования, приводящие (2.9) к виду (2.10))