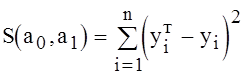Основы корреляционного и регрессионного анализа, страница 3

 или

.

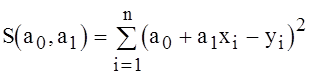Для поиска точки минимума функции приравняем ее частные производные к нулю

;

;

;

;

;

.

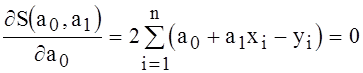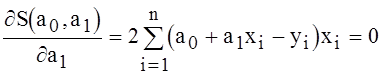Таким образом получаем систему двух линейных уравнений, неизвестными в которой являются параметры , а значения  и -берутся из исходных пар данных

.

(2.3)

Решив эту систему, найдем искомые параметры

;

.

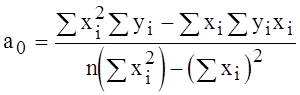(2.4)

Упрощенная форма записи для коэффициента  имеет вид

.

(2.5)

Для определения уравнения зависимости времени поставок от расстояний заполним вспомогательную таблицу 2.2.

Табл.2.2

x	y
3,5	16	12,25	56,00	15,223	0,777	0,604
2,4	13	5,76	31,2	12,297	0,703	0,494
4,9	19	24,01	93,1	18,947	0,053	0,003
4,2	18	17,64	75,60	17,085	0,915	0,837
3,0	12	9,00	36,00	13,893	-1,893	3,583
1,3	11	1,69	14,30	9,371	1,629	2,654
1,0	8	1,00	8,00	8,573	-0,573	0,328
3,0	14	9,00	42,00	13,893	0,107	0,011
1,5	9	2,25	13,50	9,903	-0,903	0,815
4,1	16	16,81	65,60	16,819	-0,819	0,671
28,9	136	99,41	435,30		-0,003	10,000

Подставив рассчитанные значения сумм из табл.2.2 в формулы (2.4) и (2.5) получим

;

.

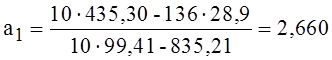Таким образом

.

Наклон линии регрессии = 2,66 мин. на милю - это количество минут, приходящееся на одну милю расстояния. Координата точки пересечения прямой с осью OY равная 5,913 минут - это время, которое не зависит от пройденного расстояния, а обуславливается всеми остальными возможными факторами, явно не учтенными при анализе.

Сумма квадратов отклонений, рассчитанная в табл.2.2, является минимальной по сравнению во всеми остальными возможными линейными функциями вида (2.2). Приблизительным, но самым простым, наглядным способом проверки удовлетворительности регрессионной модели является графическое представление отклонений. Отложим отклонения 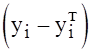 по оси OY, для каждого значения .

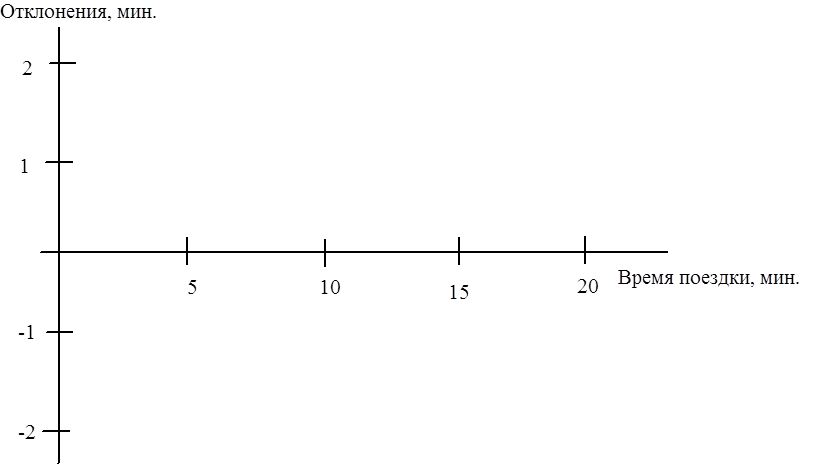
Если линейная модель близка к реальной зависимости, то отклонения будут носить случайный характер и их сумма будет близка к нулю. В рассмотренном примере 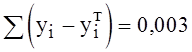. Если бы связь была нелинейной, то это четко было бы видно на рисунке, например

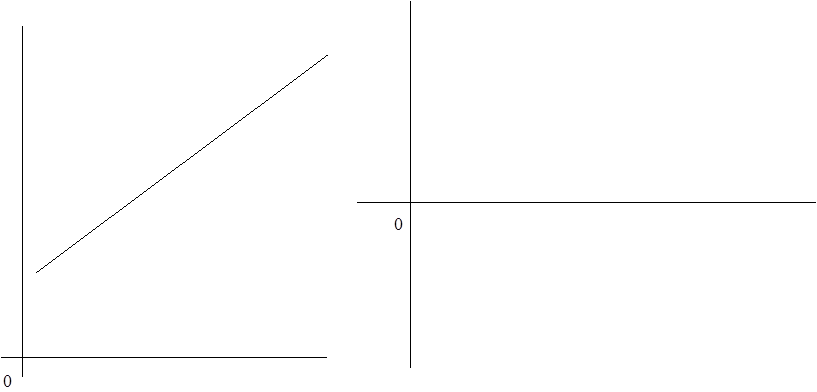
Кроме того, одним из основных предположений в методе наименьших квадратов является то, что рассеяние данных возле линии регрессии одинаково при всех значениях x. В случае, показанном на рисунке данные распределяются вдоль линии регрессии неравномерно, поэтому метод наименьших квадратов в этом случае неприменим. График отклонений при этом имеет вид.

2.3.2. Регрессия вида .

      Самостоятельно получить систему линейных уравнений типа (2.3), для определения коэффициентов ,  и .

2.4. НЕЛИНЕЙНАЯ РЕГРЕССИЯ, ПРИВОДИМАЯ К ЛИНЕЙНОЙ

На практике встречаются случаи криволинейных связей между параметрами, например

гипербола 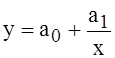                                     (2.6),

экспонента                                      (2.7).

В зависимости от значений коэффициентов графики этих функций могут выглядеть следующим образом.

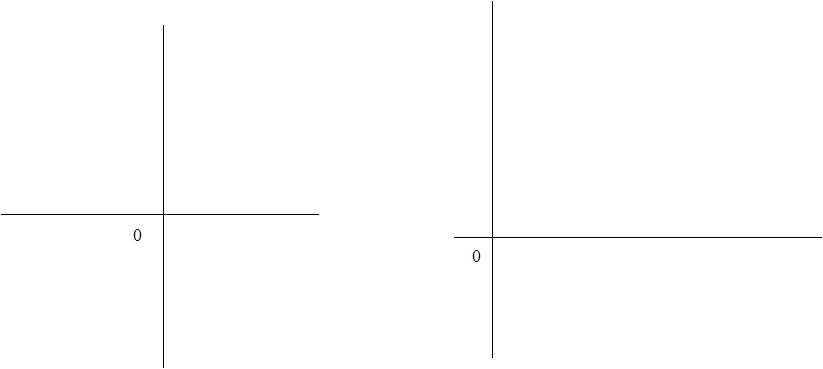
Распространенный подход к поиску численного вида функций регрессии заключается в приведении нелинейных функций к линейному виду.

При использовании модели гиперболы вводят новую переменную 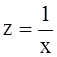, тогда (2.6) принимает линейный вид . Таким образом появляется возможность применить формулы (2.4), (2.5), в которых вместо значений  используются значения 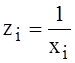, т.е. во вспомогательную таблицу вносятся соответствующие новые колонки.

;

=.

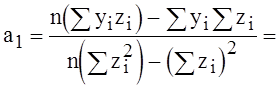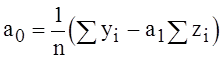Для примера о времени поставок модель регрессии (2.6) имеет следующий вид