Оптимальное распределение ресурсов, страница 9

Нечентные вершины (3,3) и (2,2) образуют положительную полуцепь. Четные вершины (3,2) и (2,3) образуют отрицательную полуцепь.

Новые значения узлов контура вычисляются так: в четных вершинах значения уменьшаются на q, в нечентных – увеличиваются на q.

Получаем новое опорное решение:

Поставщик	Потребители								Запасы	Ui
	1		2		3		4
1	120			-1		-1		-1	120	0
		2		1		3		2
2	130		0	-5	10			-2	140	1
	2	1		4	3	1		2
3		3	180		50			0	230	-2
	1	1		2	4	4		3
4		-1		-4	140		60		200	0
		3		4		2		1
5		1		-1		1	90		90	1
		0		0		0		0
Потребность	250		180		200		150
Vj	2		0		2		1

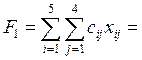1280

, что соответствует теории:

Рассчитаем новую систему потенциалов. Имеем систему уравнений:

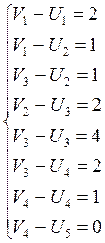
Пусть , тогда

                     

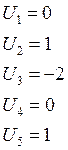
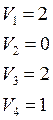
Припишем значения потенциалов соответствующим строкам и столбцам. Вычисляем значения невязок для всех клеток без перевозок. Записываем их в правый верхний угол каждой клетки. Наибольшая положительная невязка равна 3 (1,3). Строим замкнутый контур с началом в этой клетке – (1,3). В качестве остальных вершин выбираем (1,2), (3,2), (3,3).

. В нечетных вершинах значения увеличатся на q, в четных уменьшатся на q.

Получим новое опорное решение

Поставщик	Потребители								Запасы	Ui
	1		2		3		4
1	120			2		-1		-1	120	-2
	4	2	1	1		3		2
2	80		0	-2	60			-2	140	-1
		1		4		1		2
3	50		180		0	-3		-3	230	-1
	3	1	2	2		4		3
4		-1		-1	140		60		200	-2
		3		4		2		1
5		1		2		1	90		90	-1
		0		0		0		0
Потребность	250		180		200		150
Vj	0		1		0		-1

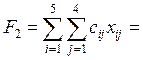1130

, что соответствует теории:

Рассчитаем новую систему потенциалов. Имеем систему уравнений:

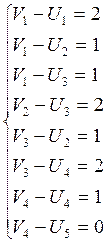
Пусть , тогда

                     

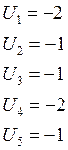
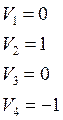
Припишем значения потенциалов соответствующим строкам и столбцам. Вычисляем значения невязок для всех клеток без перевозок. Записываем их в правый верхний угол каждой клетки. Наибольшая положительная невязка равна 2. Строим замкнутый контур с началом в клетке (2,1). В качестве остальных вершин выбираем (2,3), (1,3), (1,1).

. В нечетных вершинах значения увеличатся на q, в четных уменьшатся на q.

Получим новое опорное решение: