Оптимальное распределение ресурсов, страница 7

2)  12-ти этажные здания – от 0 до 17. Значение суммарной прибыли на нижнем пределе диапазона изменения выпуска продукции составляет 42,42 и 142,88 единицы соответственно.

7. Значение целевой функции исходной задачи и целевой функции задачи с дополнительными переменными совпали.

8.  Значения целевых функций прямой и двойственной задач совпали. Значения теневой цены в прямой задаче совпадают с решением двойственной и наоборот, т.е. прямая и двойственная задачи симметричны). Двойственные переменные  - теневая цена соответствующего ресурса.

Задача 2

Условие и постановка задачи.

Имеется четыре карьера, производящих строительные материалы, и четыре потребителя сыры строительных материалов. Известны объемы производства на каждом карьере, потребности в их продукции каждого из потреби-елей, а также стоимость перевозки 1 т продукции с 1-го карьера к J-му потребителю. Определить, при каких объемах грузоперевозок от I-го поставщика к J-му потребителю суммарная стсимость перевозок будет минимальной.

1. Решить   задачу   средствами   Excel   (Надстройка   "Поиск решения").

2. Решить задачу аналитически.

Решение транспортной задачи с помощью надстройки Excel «Поиск решения».

Решение транспортной задачи с помощью надстройки
"Поиск решений"
		Матрица цен перевозок
	Потребители
Поставщики	В1	В2	В3	В4
А1	2	1	3	2
А2	1	4	1	2
А3	1	2	4	3
А4	3	4	2	1
Аф	0	0	0	0
	Объемы перевозок
	Потребители				Запасы (Вычисленные)		Запасы (Заданные)
Поставщики	В1	В2	В3	В4		=
А1	0	120	0	0	120	=	120
А2	20	0	120	0	140	=	140
А3	230	0	0	0	230	=	230
А4	0	0	50	150	200	=	200
Аф	0	60	30	0	90	=	90
Потребности (Вычисленные)	250	180	200	150
	=	=	=	=
Потребности (Заданные)	250	180	200	150
					740	Суммарная
						стоимость
						перевозок

Аналитический метод решения транспортной задачи.

Построение математической модели.

1. Обозначим через  количество тонн строительных материалов, которые будут перевезены с i-го карьера j-ому.
2. Проверим сбалансированность задачи.

Вычислим суммарные запасы:

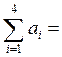690

Суммарные потребности:

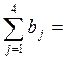780