Оптимальное распределение ресурсов, страница 8

Суммарный объем производства на карьерах меньше суммарной потребности потребителей, следовательно, имеем транспортную задачу открытого типа (несбалансированную транспортную задачу).

3. Сведем задачу к сбалансированной, введя фиктивный карьер с объемом производства, равным недостающему запасу. Стоимость перевозок из фиктивного карьера всем j-м потребителям примем равной 0.

Сбалансированная транспортная матрица задачи

Поставщик	Потребители				Запасы
	В1	В2	В3	В4
А1	2	1	3	2	120
А2	1	4	1	2	140
А3	1	2	4	3	230
А4	3	4	2	1	200
Аф	0	0	0	0	90
Потребность	250	180	200	150	780

4. Формальная ЦФ, т.е. суммарные затраты на все возможные перевозки строительных материалов, учитываемые в модели, задается следующим выражением:

5. Т.к. весь груз должен быть вывезен и все потребности удовлетворены полностью, становятся очевидными следующие ограничения:

Фазовые ограничения:

             

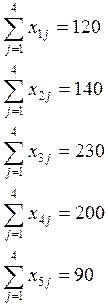
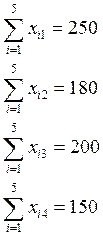
Естественные ограничения:

Построение исходного опорного плана.

Построим опорный план методом северо-западного угла. Для этого заполним ячейку (1,1). Занесем меньшее из чисел  и , т.е.

Поставщик	Потребители				Запасы
	В1	В2	В3	В4
А1	120 2	1	3	2	120
А2	130 1	10 4	1	2	140
А3	1	170 2	60 4	3	230
А4	3	4	140 2	60 1	200
Аф	0	0	0	90 0	90
Потребность	250	180	200	150	780

В результате имеем таблицу с восемью заполненными клетками, что соответствует теории:

Суммарная стоимость перевозок для полученного опорного плана:

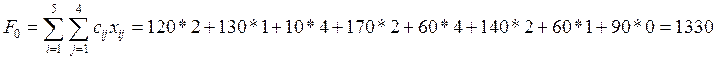
Рассчитаем систему потенциалов для этого решения.

Для определения  имеем следующую систему уравнений:

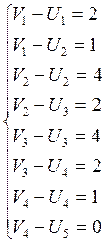
Имеем 8 уравнений и 9 неизвестных. Значение одной из неизвестных величин (любой) можно задать произвольным образом. Положим . Тогда остальные величины будут равны:

        

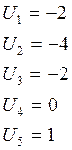
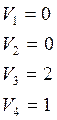
Припишем значения потенциалов соответствующим строкам и столбцам. Введем дополнительный столбец  и дополнительную строку  и занесм вычисленные значения потенциалов в полученные клетки.

Поставщик	Потребители								Запасы	Ui
	1		2		3		4
1	120			1		1		1	120	-2
		2		1		3		2
2	130		10			5		3	140	-4
		1	4	4	1	1		2
3		1	170		60			0	230	-2
		1	3	2	2	4		3
4		-3		-4	140		60		200	0
		3		4		2		1
5		-1		-1		1	90		90	1
		0		0		0		0
Потребность	250		180		200		150
Vj	0		0		2		1

Вычислим значения невязок для всех клеток без перевозок по формуле (3.7) Методических рекомендаций. Запишем их в правый верхний угол каждой клетки. В ряде клеток наблюдаются нарушения (положительные невязки). Выбираем клетку, в которой наблюдается наибольшее превышение, равное 5 – (3,2) . Строим замкнутый цикл с началом в этой клетке. В качестве остальных вершин выберем и пронумеруем клетки (3,3), (2,3), (2,2) (выделены красным цветом).