Контрольная работа № 1. Отчет по задаче оптимального распределения ресурсов и транспортной задаче

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ

Государственное образовательное учреждение высшего профессионального образования

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ГОРНЫЙ ИНСТИТУТ

ИМ. Г.В. ПЛЕХАНОВА

(технический университет)

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИРОВАНИЕ     

Контрольная работа №1

Отчет по задаче оптимального распределения ресурсов

и транспортной задаче

Санкт-Петербург

2010

Оглавление

1.ОПТИМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ РЕСУРСОВ.. 3

1.1.Задание. 3

1.2.Математическая модель задачи. 3

1.3.Решение задачи симплекс-методом.. 4

1.4.Решение задачи в Microsoft Excel (надстройка «Поиск решения») 8

1.5.Решение двойственной задачи в Microsoft Excel 11

1.6.Экономический анализ полученных результатов. 12

2.ТРАНСПОРТНАЯ ЗАДАЧА.. 17

1.2.Задание. 17

1.2.Математическая модель задачи. 17

1.3.Решение задачи в Microsoft Excel (надстройка «Поиск решения») 18

1.4. Аналитическое решение транспортной задачи. 21

1.4.1. Определение исходного опорного решения. 21

1.4.2. Построение оптимального решения методом потенциалов. 22

1.ОПТИМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ РЕСУРСОВ

1.1.Задание

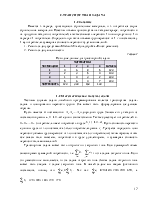
Строительная фирма может возводить типовые жилые здания различной этажности: 16-ти, 12-ти,9-ти и 6-ти этажные. Реализация единицы площади каждого вида жилья дает прибыль в 10, 6 , 3 и 3 условных единиц соответственно. Перечень ресурсов, их количество и нормы расхода для производства единицы площади жилья приведены в таблице 1.      

Таблица 1

Исходные данные для задачи распределения ресурсов

Составить план строительства  или реконструкции жилья строительной фирмой. Тип застройки, прибыль от их реализации 1 кв. м. жилья и нормы расхода основных ресурсов приведены для каждого варианта. Цель  планирования - достижение максимальной прибыли. Считать  единицу измерения объема выпуска достаточно большой (например, тысячи квадратных метров) – т.е. результат не обязательно целочисленный.

1. Решить задачу аналитически симплекс-методом.
2. Решить задачу средствами  Microsoft Excel (надстройка «Поиск решения»).
3. Составить двойственную задачу, решить ее. Сравнить полученное решение с решением задачи в п.1-2. дать экономическую интерпретацию полученных результатов.

1.2.Математическая модель задачи

Составим математическую модель для данной задачи. Пусть  - количество выпускаемой продукции j-типа, j=1,2,3,4. Как видно из таблицы 1, для выпуска одного квадратного метра 16-ти этажного жилья требуется 3 единицы электроэнергии, значит, для выпуска всего количества 16-ти этажного жилья потребуется единиц электроэнергии, для строительства всего количества 12-ти этажного жилья потребуется  единиц электроэнергии и. т. д. Таким образом, ограничение по электроэнергии будет иметь вид:. В этом ограничении левая часть показывает потребность в ресурсе, а правя- его имеющееся количество в наличии.

Аналогично можно составить ограничения для других ресурсов и написать зависимость для целевой функции. Тогда математическая модель будет иметь следующий вид:

1.3.Решение задачи симплекс-методом

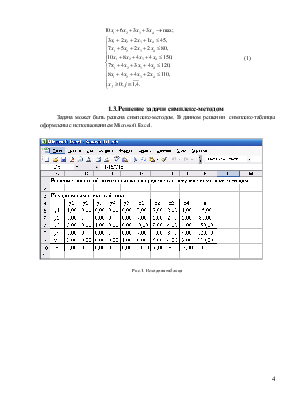
Задача может быть решена симплекс-методом. В данном решении  симплекс-таблицы оформлены с использованием Microsoft Excel.

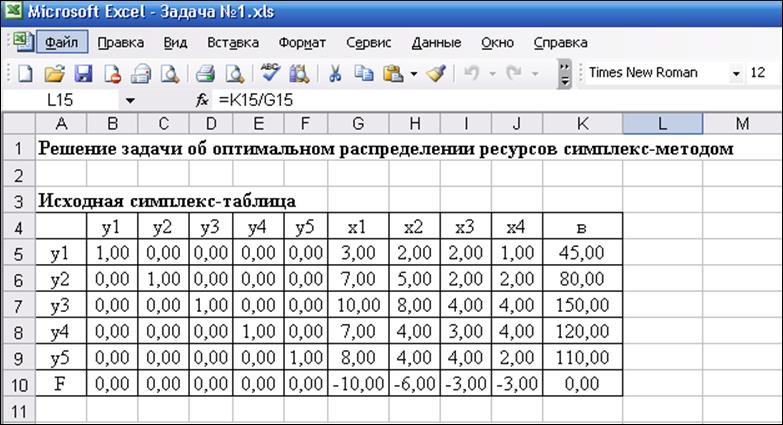
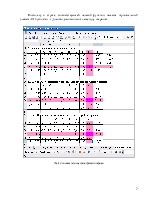
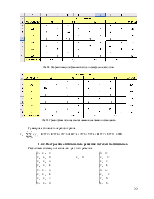
Рис.1. Исходная таблица

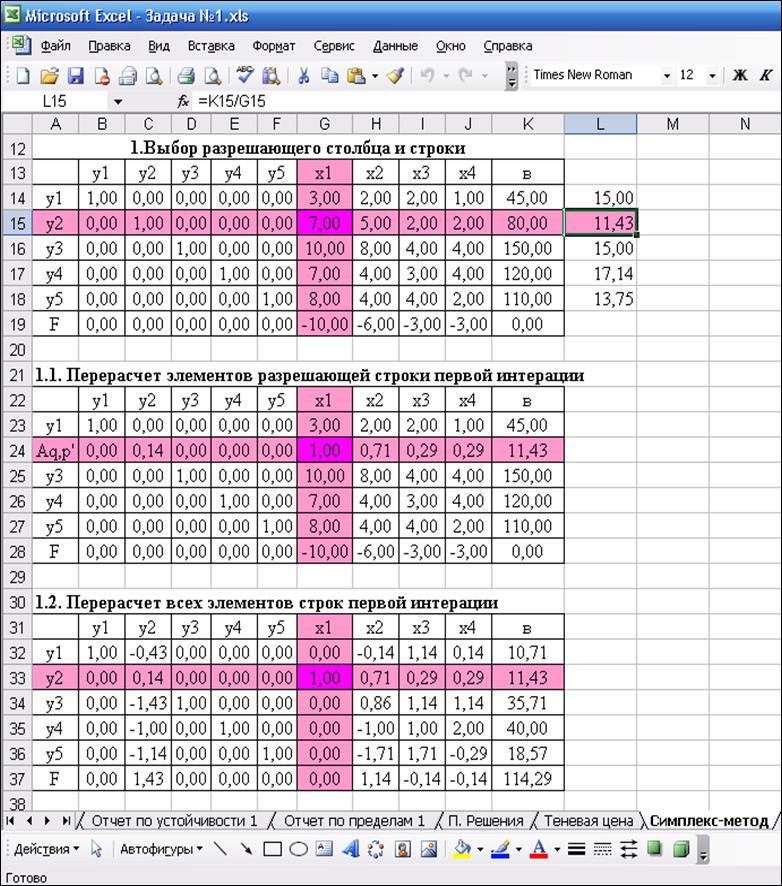
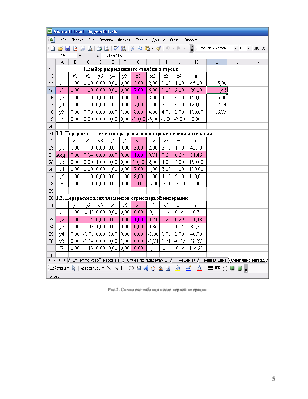
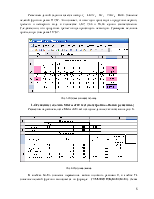
Рис.2. Симплекс-таблица после первой итерации

Поскольку в строке, соответствующей целевой функции, имеется два отрицательных элемента -0,14 (столбцы и ) необходимо выполнить еще одну итерацию.

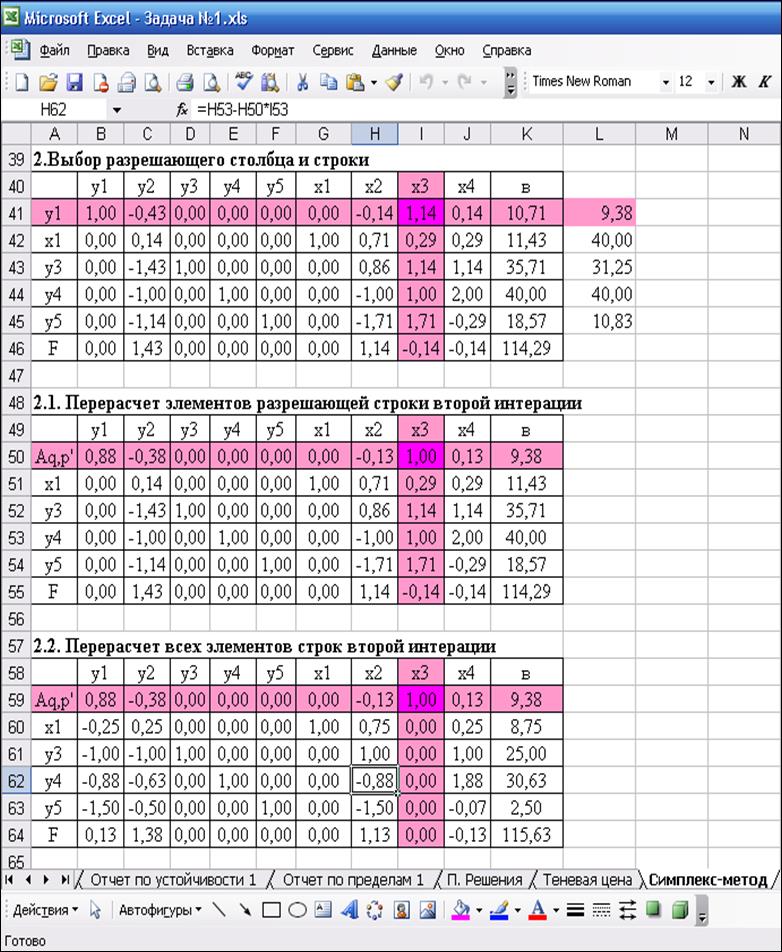
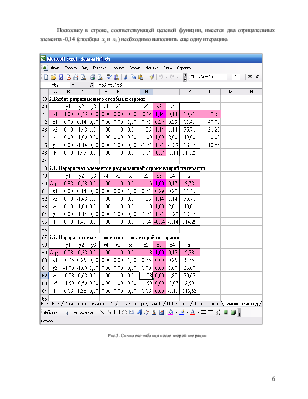
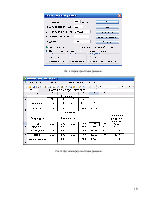
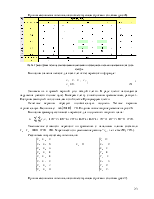
Рис.3. Симплекс-таблица после второй итерации

Поскольку в строке, соответствующей целевой функции, имеется отрицательный элемент -0,13 (столбец   ) необходимо выполнить еще одну итерацию.

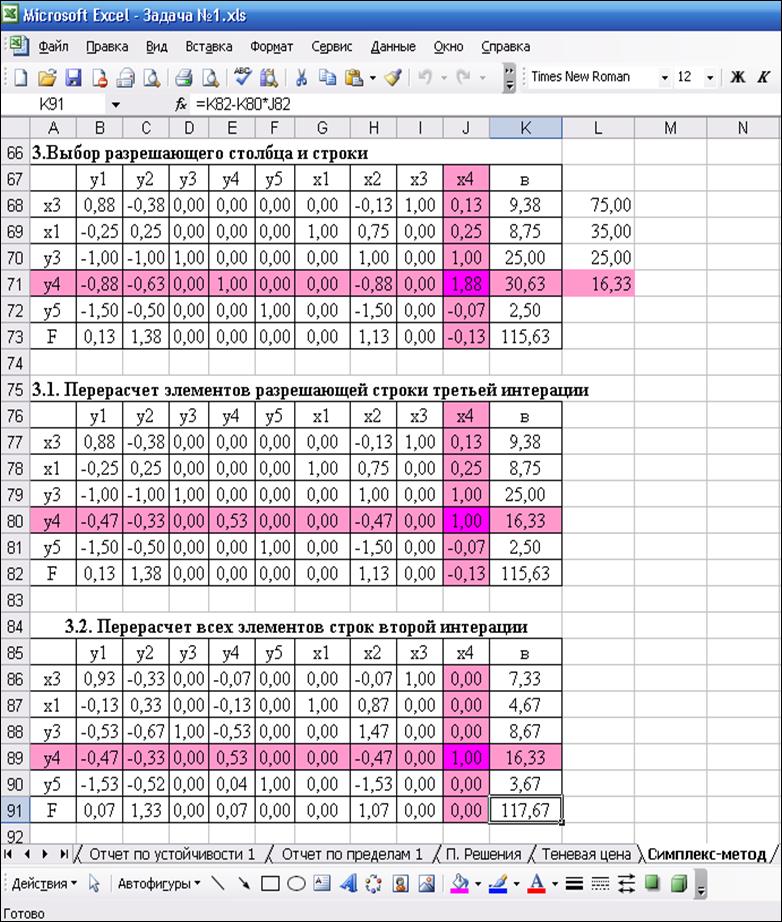
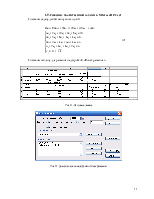
Рис.4. Симплекс-таблица после третьей итерации

Решением данной задачи является набор  Значение целевой функции равно 117,67. Это означает, что выгодно производить продукцию первого, третьего и четвертого вида в количестве 4,67; 7,33 и 16,33 единиц соответственно. Следовательно, что продукцию третьего вида производить невыгодно. Суммарная величина прибыли при этом равна 117,67 .

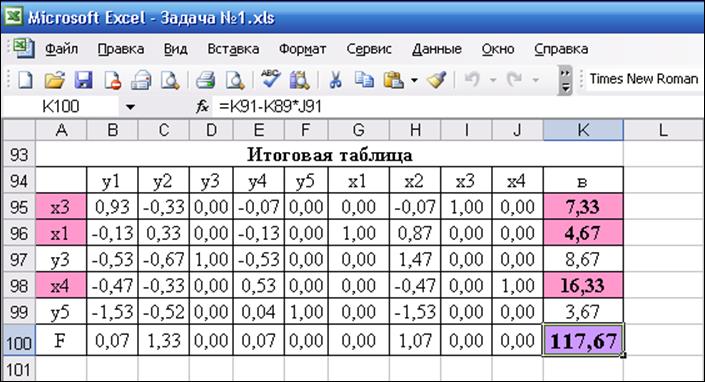
Рис. 5. Итоговая симплекс-таблица

1.4.Решение задачи в Microsoft Excel (надстройка «Поиск решения»)

Разместим на рабочем листе Microsoft Excel  исходные данные, как показано на рис. 6 .

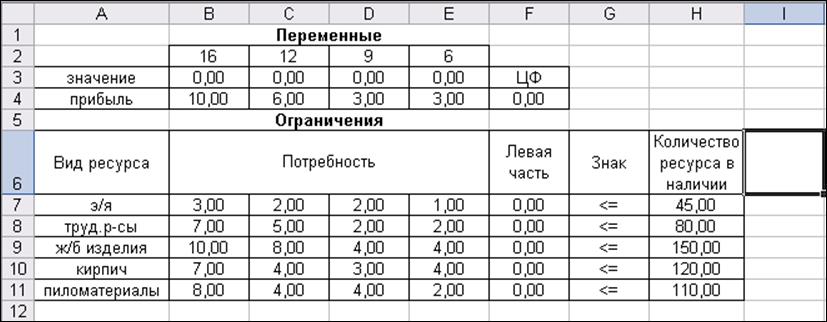
Рис. 6. Исходные данные

В ячейках B3:E3 значения переменных можно положить равными 0, в ячейке F4 значение целевой функции вычисляется по формуле =СУММПРОИЗВ(B3:E3;B4:E4). Левая часть ограничений вычисляется следующим образом: в ячейку F7 заносится формула =СУММПРОИЗВ($B$3:$E$3;B7:E7), после чего она копируется в ячейки F8: F11.

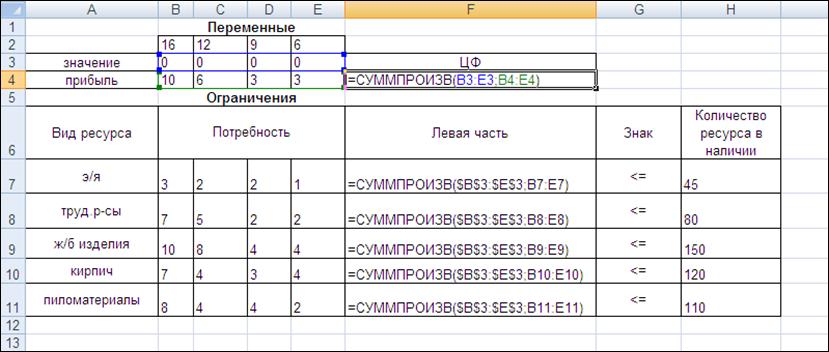
Рис. 7. Режим отображения формул

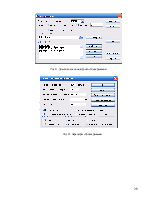
Активизируем надстройку «Поиск решения»  из пункта меню сервис и заполним диалоговое окно, как показано на рис. 8,9.