Контрольная работа № 1. Отчет по задаче оптимального распределения ресурсов и транспортной задаче, страница 3

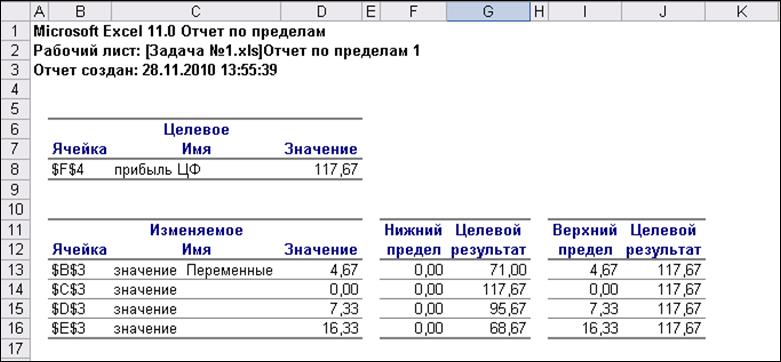
Рис.16. Отчет по пределам

4. Отчет по устойчивости. Отчет по устойчивости (рис. 17) состоит из двух таблиц. В первой таблице приводятся:
• оптимальный план задачи. В нашем случае, чтобы получить максимальную выручку в размере 117,67 единиц, нужно производить продукцию первого, третьего и четвертого вида в количестве 4,67; 7,33 и 16,33 единиц соответственно.
• нормированная стоимость касается неизвестных плана. Она показывает, на сколько изменится целевая функция при принудительном включении единицы этой продукции в оптимальное решение. Значение отлично от 0, когда соответствующий вид продукции не входит в оптимальный план, и наоборот. В нашей задаче можно сказать, что при принудительном строительстве 1 кв. м. жилья в 12-ти этажном жилом здании целевая функция изменится на 1,07 единицы.
• коэффициенты ЦФ;
• предельные значения приращения коэффициентов целевой функции, при котором сохраняется структура оптимального решения.  В нашем примере структура оптимального решения не меняется при изменении величины прибыли в следующих диапазонах:

- для 16-ти этажного жилья – [10-1,23; 10+0,5]=[8,77;10,5];

- для 12-ти этажного жилья – [6-1E+30; 6=1,07], но так как величина прибыли ограничена снизу нулем, получаем диапазон  [0;7];

- для 9-ти этажного жилья – [3-0,07;3+1]=[2,93;4];

- для 6-ти этажного жилья – [3-0,13;3+0,14]=[2,87;3,14].

Во второй таблице приводятся аналогичные значения для ограничений:

• величина использованных ресурсов;
• теневая цена, которая показывает, как изменится целевая функция при изменении ресурсов на единицу. Для ресурсов, использованных не полностью, теневая цена равна 0, и наоборот;
• значения приращения ресурсов, при которых сохраняется структура оптимального решения.

Что касается данной задачи, то если бы у нас была возможность увеличить количество электроэнергии на 1 единицу, то целевая функция увеличилась бы на 0,07 единиц. Если увеличить трудовые ресурсы на 1 единицу, то ЦФ увеличится на 1,33 единицы. Если же увеличить количество кирпича на 1 единицу, то ЦФ увеличится на 0,07 единиц.

Структура оптимального решения не изменится при изменении фактического наличия ресурсов:

- электроэнергия в диапазоне [45-7,86;45+6,15]=[37,14;51;15];

- трудовые ресурсы в диапазоне [80-14;80+13]=[66;93];

-железобетонные изделия в диапазоне [150-8,67;150+1E+30]=[0;141,33];

- кирпич в диапазоне [120-30,63;120+16,25]=[89,37;136,25];

- пиломатериалы в диапазоне [110-10,67;110+1E+30]=[0;99,33].

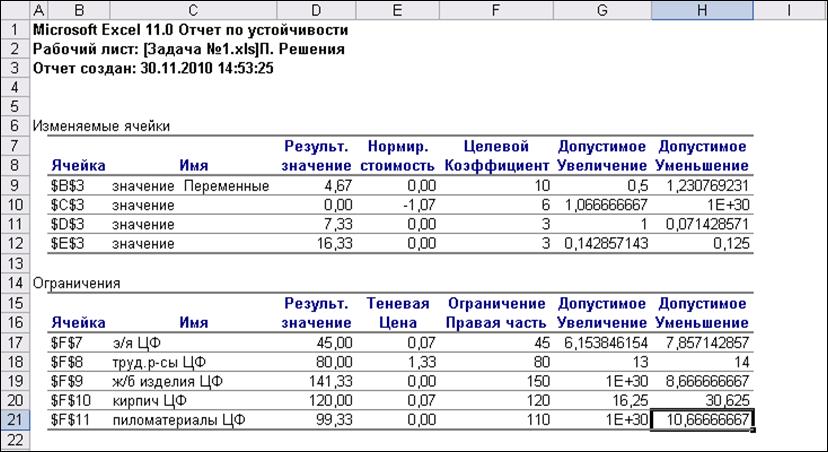
Рис.17. Отчет по устойчивости 1 (прямая задача)

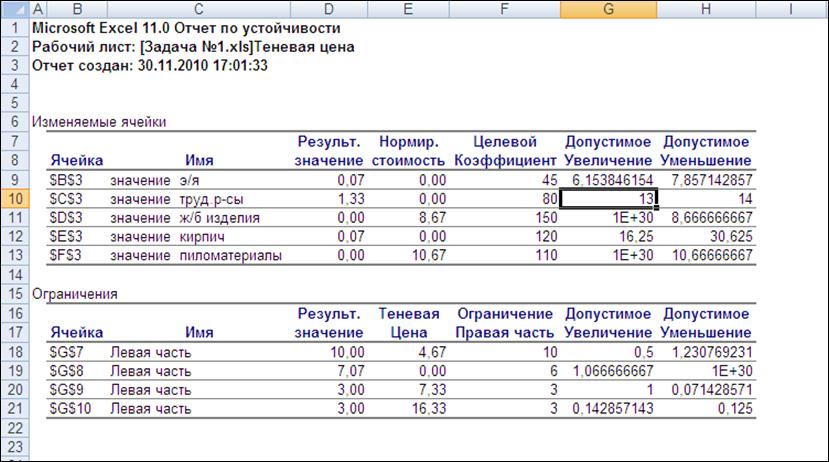
Рис.18. Отчет по устойчивости 2 (двойственная задача)

2.ТРАНСПОРТНАЯ ЗАДАЧА

1.2.Задание

Имеется 4 карьера, производящих строительные материалы, и 4 потребителя сырья строительных материалов. Известны объемы производства на каждом карьере, потребности в их продукции каждого из потребителей, а также стоимость перевозки 1 тонны продукции с I–го карьера к J–потребителю. Определить при каких объемах грузоперевозок от I– го поставщика у J–му потребителю суммарная стоимость перевозок будет минимальной.

1. Решить задачу средствами Microsoft Excel (надстройка «Поиск решения»).
2. Решить задачу аналитически.

Таблица 2

Исходные данные для транспортной задачи

1.2.Математическая модель задачи

Частным случаем задачи линейного программирования является транспортная задача- задача о планировании перевозки грузов. Она может быть сформулирована следующим образом.