Контрольная работа № 1. Отчет по задаче оптимального распределения ресурсов и транспортной задаче, страница 4

Пусть имеется m поставщиков  однородного груза. Запасы его у каждого из поставщиков равны единиц соответственно. Также существует потребителей n, , j-потребитель имеет потребность в грузе . Пусть стоимость перевозки единицы груза от i-го поставщика j-тому потребителю равна . Требуется определить план перевозок (объемы грузоперевозок  от i-го поставщика j-му потребителю) таким образом, чтобы все запасы были вывезены, потребности в грузе удовлетворены, и суммарная стоимость перевозок была минимальной.

Транспортная задача может быть открытого и закрытого типа. Если суммарный объем запасов равен суммарной потребности, т.е. 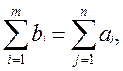 то эта задача закрытого типа. Если это равенство не выполняется, то эта задача открытого типа. Любая задача открытого типа может быть сведена к задаче закрытого типа. В нашей задаче мы введем фиктивного поставщика, потому что 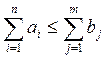. Так как 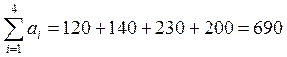, а .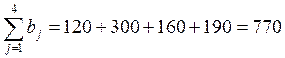

Целевая функция может быть определена соотношением:

;

((3)

где F – суммарная стоимость всех перевозок;

 объем грузоперевозок.

Фазовые и естественные ограничения:

((4)

Тогда исходная таблица примет вид, который показан в таб. 3.

Таблица 3

ПОСТАВЩИКИ	ПОТРЕБИТЕЛИ				ЗАПАСЫ
	В1	В2	В3	В4
А1	4	6	8	5	120
А2	2	3	5	4	140
А3	1	4	3	2	230
А4	5	6	4	7	200
А5	0	0	0	0	80
ПОТРЕБНОСТЬ	120	300	160	190

1.3.Решение задачи в Microsoft Excel (надстройка «Поиск решения»)

Решим данную задачу в Microsoft Excel, используя надстройку «Поиск решения». Схема решения транспортной задачи совпадает с общей схемой решения любой задачи линейного программирования.

Лист  Microsoft Excel заполним, как показано на рис. 18, учитывая тот факт, что мы ввели фиктивного поставщика для того, чтобы свести задачу открытого типа к задаче закрытого типа.

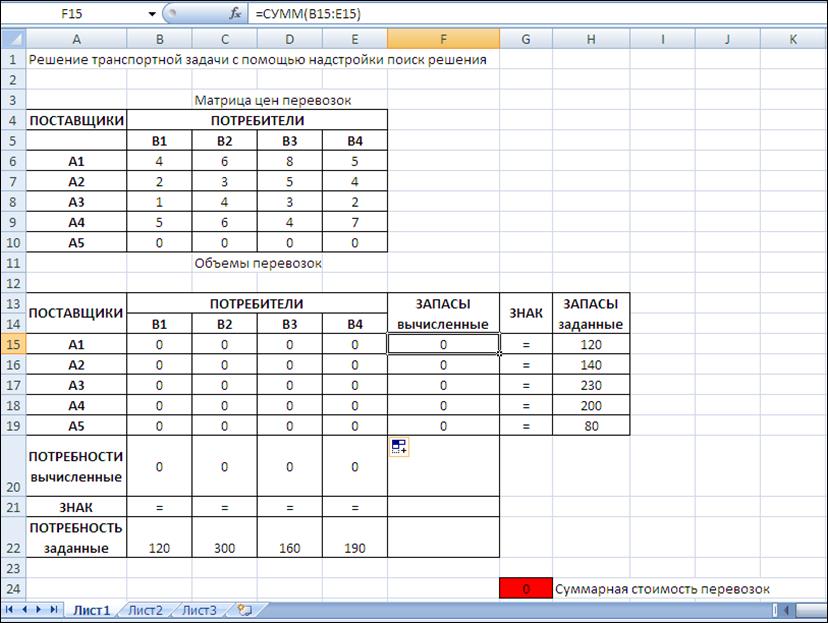
Рис. 19. Исходные данные

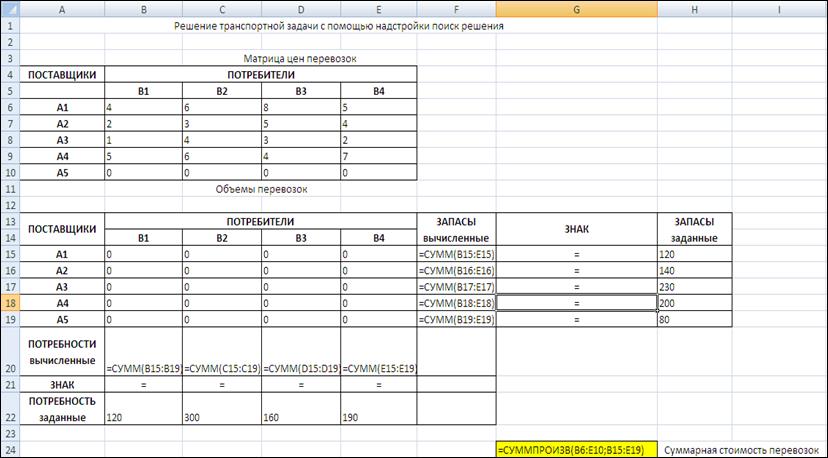
Рис. 20. Исходные данные

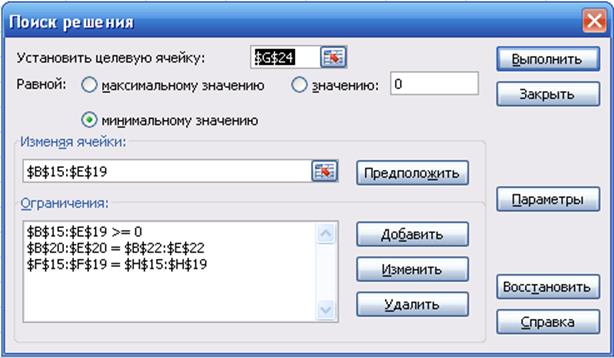
Рис. 21. Диалоговое окно надстройки «Поиск решения»

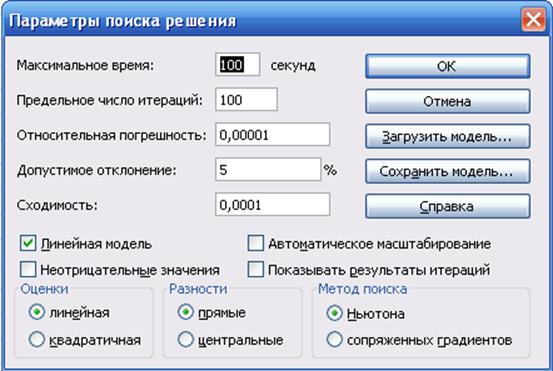
Рис. 22. Параметры «Поиска решения»

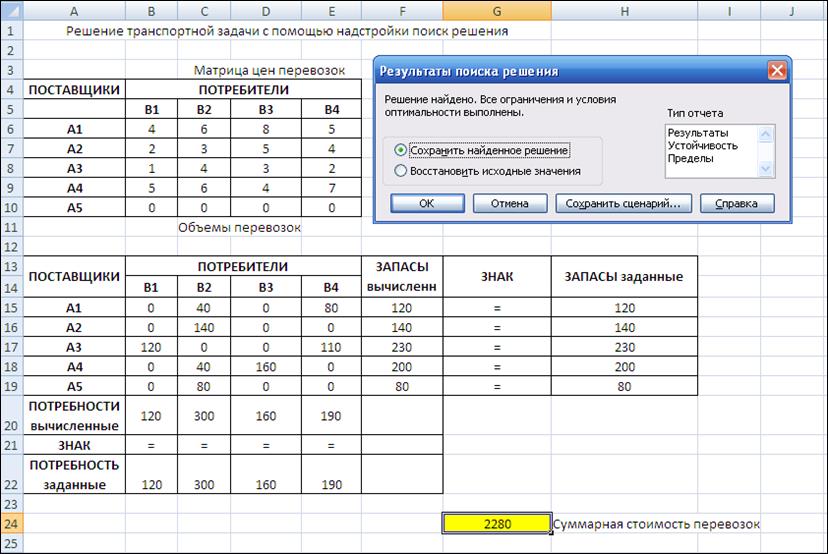
Рис.23. Результаты работы «Поиска решения»

1.4. Аналитическое решение транспортной задачи

Решение получается путем преобразования транспортной таблицы по определенным правилам.

Решение строится в два этапа:

• На первом этапе отыскивается исходное опорное решение;
• На втором этапе методом последовательных итераций ищется оптимальное решение.

1.4.1. Определение исходного опорного решения

Построим опорное решение методом «северо-западного угла». В результате имеем таблицу с семью заполненными клетками, что не соответствует теории: m+n-1=5+4-1=8. В таком случае нельзя построить систему потенциалов, и такой план называется вырожденным (рис. 24).

Строим новый опорный план, представленный на рис. 25. В результате получен опорный план, который является допустимым, так как все грузы вывезены, потребность потребителей удовлетворена, то план соответствует системе ограничений транспортной задачи. Подсчитаем число занятых клеток таблицы, их 8, а должно быть m + n - 1 = 8. Следовательно, опорный план является невырожденным.

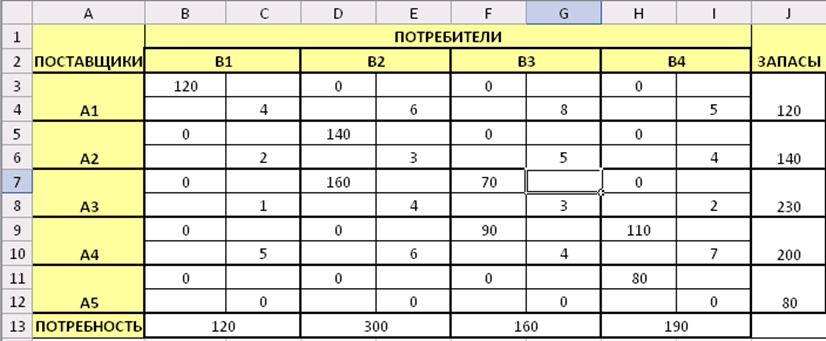
Рис.24. Опорный план, построенный методом «северо-западного угла»

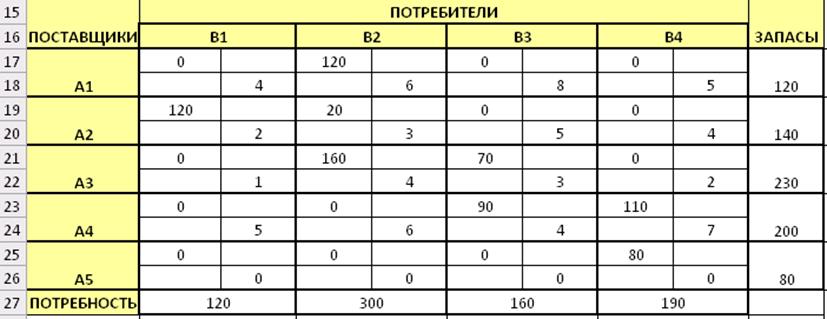
Рис.25. Транспортная таблица с вычисленными значениями потенциалов

Суммарная стоимость перевозок равна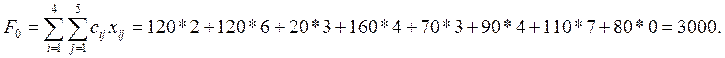

1.4.2. Построение оптимального решения методом потенциалов

Рассчитаем систему потенциалов для этого решения.

Припишем значения потенциалов соответствующим строкам и столбцам (рис.26).

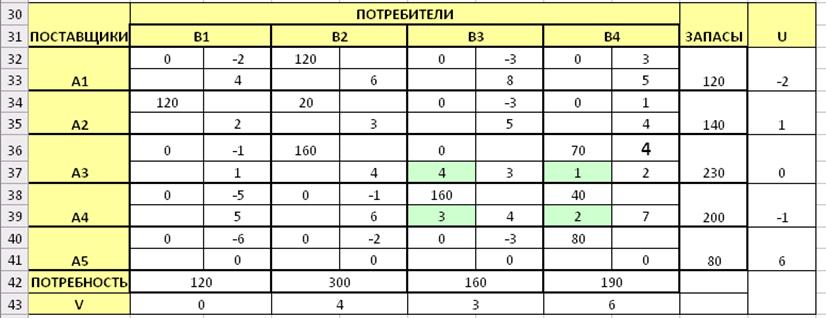
 Рис.26. Транспортная таблица с вычисленными значениями потенциалов и новыми значениями для узлов контура

Вычислим значения невязок для всех клеток без перевозок по формуле:

;

((5)

Запишем их в правый верхний угол каждой клетки. В ряде клеток наблюдаются нарушения (невязки больше нуля). Выберем клетку с наибольшим превышением, равную 4. Построим замкнутый цикл с началом в этой клетке. Пронумеруем клетки.