На рис. 10 показано полученное решение. При этом в ячейках диапазона B3:E3 находятся искомые значения объемов выпуска продукции, соответствующие оптимальному плану. В ячейке F4 находится значение целевой функции (ЦФ), которое соответствует оптимальному плану.
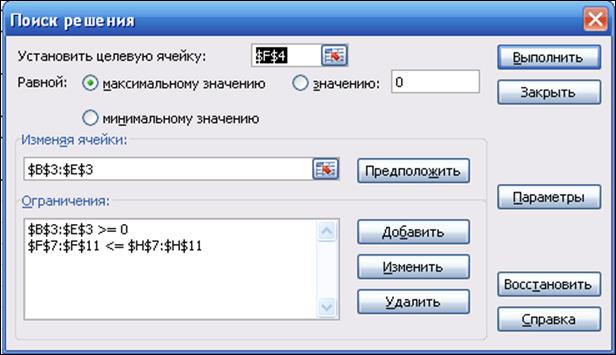
Рис. 8. Диалоговое окно надстройки «Поиск решения»
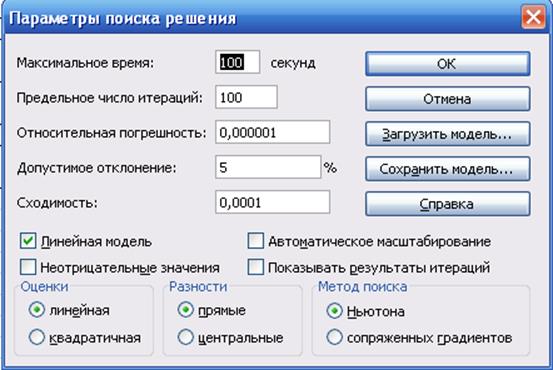
Рис. 9. Параметры «Поиска решения»
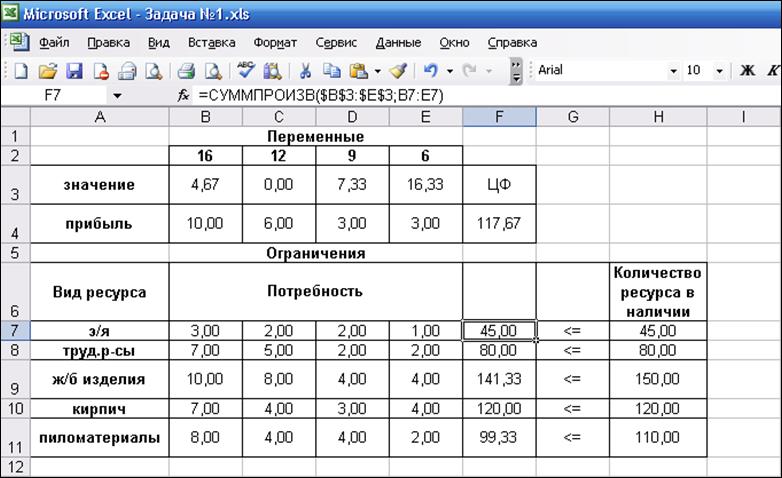
Рис.10. Результаты работы «Поиска решения»
Составим задачу двойственную исходной:
|
|
(2) |
Составим таблицу для решения надстройкой «Поиск решения».
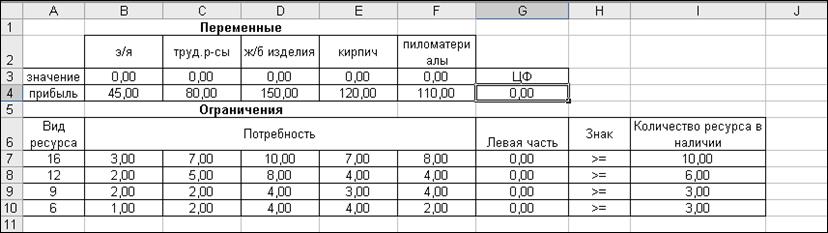
Рис. 11. Исходные данные
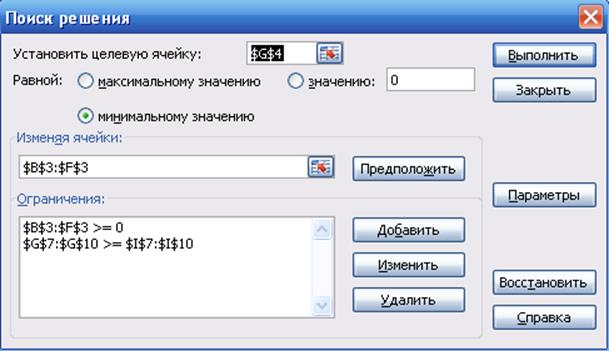
Рис. 12. Диалоговое окно надстройки «Поиск решения»
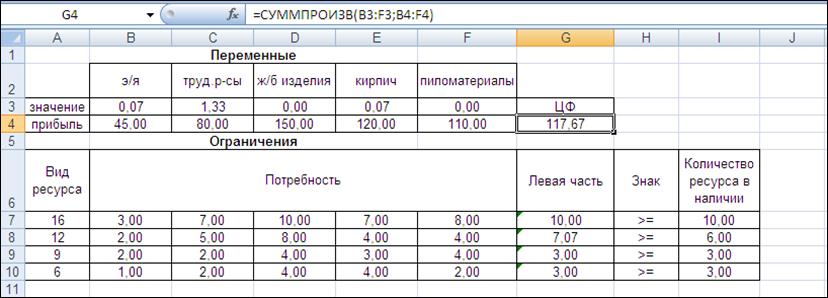
Рис.13. Результаты работы «Поиска решения»
Значения целевых функций
прямой и двойственной задач совпали. Значения теневой цены в прямой задаче
совпадают с решением двойственной, и наоборот (в этом заключается
симметричность прямой и двойственной задач). Таким образом, смысл двойственных
переменных ![]() - это теневая цена соответствующего
ресурса.
- это теневая цена соответствующего
ресурса.
Анализ оптимального решения можно проводить после успешного решения задачи, когда на экране появляется диалоговое окно «Результаты поиска решения» с сообщением «Решение найдено» (рис. 14). С помощью этого диалогового окна можно вызвать отчеты трех типов: результаты, устойчивость и пределы.
Рис. 14. Диалоговое окно «Результаты поиска решения»
целевой функции равно 117,67. Это означает, что выгодно производить продукцию первого, третьего и четвертого вида в количестве 4,67; 7,33 и 16,33 единиц соответственно. Следовательно, что продукцию третьего вида производить невыгодно. Суммарная величина прибыли при этом равна 117,67 .
Часть 1 приводит сведения о целевой функции до начала вычислений. Часть 2 приводит значения искомых переменных до и после решения задачи. Часть 3 показывает результаты оптимального решения для ограничений и граничных условий.
Для ограничений в графе «Формула» приведены зависимости, которые были введены в окно «Поиска решения»; в графе «Значение» приведены величины использованного ресурса; в графе «Разница» - количество неиспользованного ресурса. Если ресурс использован полностью, то в графу «Статус» заносится сообщение «связанное», если не полностью - «не связан». Для граничных условий приводятся аналогичные величины, только вместо величины неиспользованного ресурса показана разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием.
В нашей задаче для получения максимальной прибыли необходимо производить 4,67 единиц 16-ти этажного жилья, 7,33 единиц 9-ти этажного жилья и 16,33 единиц 6-ти этажного жилья, при этом электроэнергия, трудовые ресурсы и кирпич используются полностью, а железобетонные изделия и пиломатериалы – нет.
Поскольку трудовые ресурсы использованы полностью и привлечь для дополнительных работ их нельзя, оставшиеся ресурсы (железобетонные изделия и пиломатериалы) можно реализовать на продажу по выгодной цене, либо сохранить для следующих строительных работ, как дополнительный ресурс.
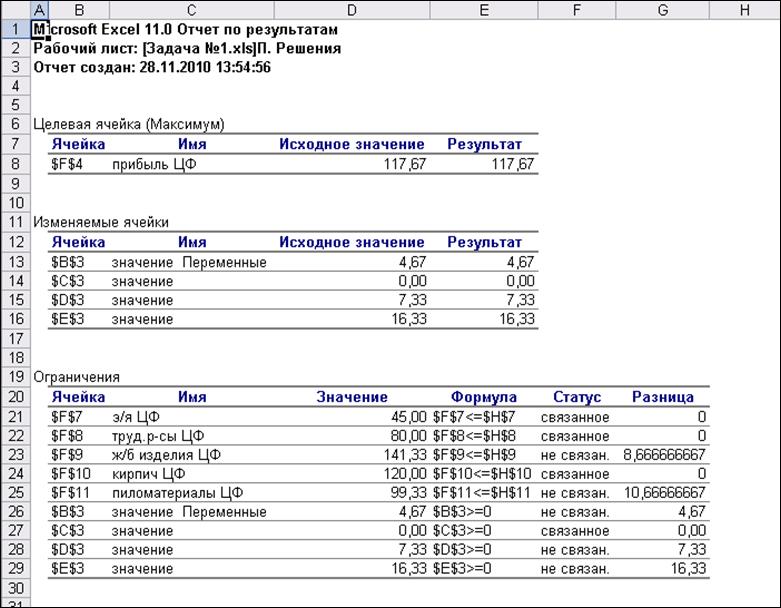
Рис. 15. Отчет по результатам
может изменяться выпуск продукции, вошедшей в оптимальное решение, при сохранении структуры оптимального решения. Отчет по пределам состоит из двух частей, что касаются значений ЦФ (Целевое) и плана (Изменяемое). Нижний предел - наименьшее значение, которое может принять неизвестное (в нашем случае количество единиц различной этажности зданий имеет Нижний предел 0, поскольку мы в Параметрах Поиска решений отметили Неотрицательные значения) Первый целевой результат - это значение, которое будет в целевой ячейке (прибыль), если неизвестное будет равно Нижнему пределу. Верхний предел - это наибольшее значение, которое может содержать неизвестные, чтобы получить максимальную ЦФ. Второй целевой результат – это значение, которое будет в целевой ячейке (прибыль), если неизвестные будут равны Верхнему пределу.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.