Основы теории производства и издержек, страница 4

Нужно перевести всё в трудодни:

1 корзина еды = 0.1 трудодня

1охапка дров = 0.05 трудодня

1 топор = 0.2 трудодня

1 бумеранг = 0.1 трудодня

1 свободный день = 1 корзина еды + 3 охапки дров = 0.25 трудодня

Три основных вопроса, решаемых при анализе межотраслевого баланса:

1. От чего зависит объём промежуточной продукции каждой отрасли.
2. Как по заданным валовым выпускам рассчитать конечную продукцию каждой отрасли (по  найти ).

3.  Как решить обратную задачу: по заданной конечной продукции найти объём валовых выпусков.

 — коэффициент прямых затрат:

.

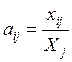 — матрица прямых затрат.

 — показывает, сколько единиц продукции -ой отрасли непосредственно затрачивается в качестве средств производства на выпуск единицы продукции -ой отрасли.

 — матрица полных затрат.

Элементы этой матрицы показывают, сколько в целом нужно произвести продукции -ой отрасли для выпускав сферу конечного потребления единицы продукции -ой отрасли.

 — матрица косвенных затрат.

Матрица косвенных затрат характеризует непрямые затраты, вызванные увеличением объёмов производства. Она показывает, сколько единиц продукции -ой отрасли входит в непрямые затраты при увеличении производства в -ой отрасли на единицу.

 — продуктивная матрица, если , где  — полуположительный вектор.

Полуположительный вектор — это неотрицательный вектор, не равный нулевому.

Теорема

Если  — продуктивная матрица, то для любого вектора конечного выпуска уравнение  имеет единственное неотрицательное решение.

Следствие 1

Если матрица прямых затрат продуктивная, то матрица  будет невырожденной.

Следствие 2

Матрица  является продуктивной тогда и только тогда, когда матрица полных затрат неотрицательная.

Для каждого набора продуктов можно указать, какой из этих наборов наиболее предпочтителен для потребителей. Т. е. существует непрерывная функция  — функция полезности. Полезность каждого вида продукции, производимой в МОБ, задаётся с помощью какого-то положительного числа . Тогда полезность вектора конечного выпуска есть

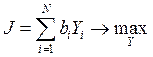, ограничения — балансовые соотношения.

Получаем задачу линейного программирования. Ограничение сверху: валовые выпуски отраслей е могут увеличиваться неограниченно.

 — максимально возможные затраты труда в -ой отрасли;

 — удельные трудовые затраты -ой отрасли;

 — совокупный объём имеющихся производственных мощностей в -ой отрасли.

, , .

Дискретная динамическая модель МОБ

Конечный продукт каждой отрасли расходуется на 3 составляющие: накопление и личное и общественное потребление. Последние 2 слагаемых объединим: будем обозначать как  (для -ой отрасли). Накопление — та часть, что идёт на развитие.

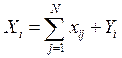
 — календарный период времени, для которого строится межотраслевой баланс;

 — мощность -ой отрасли для момента времени  (т. е. максимально возможное производство);

 — прирост мощности -ой отрасли для соответствующего момента времени;

,

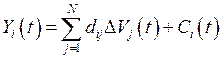 — показатели удельных фондообразующих затрат: показывают, сколько продукции -ой отрасли расходуется на единичный прирост основных фондов -ой отрасли

,

 — коэффициент амортизации;

 — валовой выпуск

,

.

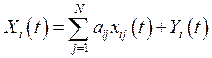В основу дискретной динамической модели положено 3 гипотезы:

1. Для развития мощностей в каждой отрасли используется только один вариант соответствующей технологии — он задаётся коэффициентом фондообразующих затрат.
2. Значения этих коэффициентов не меняются во времени на рассматриваемом интервале .
3. Затраты продукции на развитие мощностей в момент времени  обеспечивают прирост мощностей уже в следующий момент времени.