Ситуация при ![]() называется ситуацией с постоянной
отдачей от масштаба.
называется ситуацией с постоянной
отдачей от масштаба.
Производственная функция называется однородной степени k, если выполняется равенство (*).
Упражнение Доказать, что функция Кобба-Дугласа
![]()
является однородной степени ![]() (
(![]() ).
).
Введём ряд предположений о производственных свойствах функций:
Упражнение Привести экономическую интерпретацию первых трёх свойств.
![]() в случае
в случае ![]()
![]() ,
, ![]()
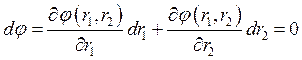
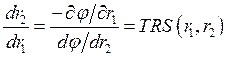 —
—
технологическая норма замещения (предельная норма замещения) — показывает пропорцию, в которой необходимо заменить один фактор другим, чтобы сохранить уровень выпуска.
Закон убывающей TRS:
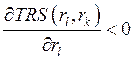 .
.
Упражнение Показать, что для функции Кобба-Дугласа уравнение изокванты имеет вид:
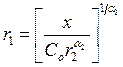 , где
, где ![]() — объём выпуска,
— объём выпуска,
![]() .
.
Производственная функция с частичной вариацией факторов —
![]() .
.
На сколько
увеличится выпуск при малом увеличении расхода одного из факторов при
неизменном количестве остальных факторов — это предельный продукт
фактора ![]() :
:
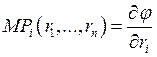 .
.
Упражнение
Найти предельный продукт фактора ![]() для функции
Кобба-Дугласа.
для функции
Кобба-Дугласа.
Отдача от масштаба описывает, что происходит при увеличении расхода всех факторов, а предельный продукт — при росте расхода одного фактора.
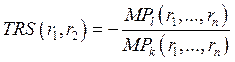 .
.
При росте расхода какого-либо одного фактора выпуск будет расти, но расти с убывающим темпом:
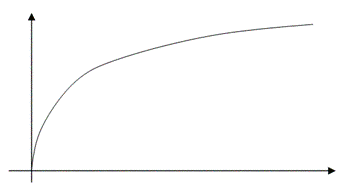
Пример Заготовка грибов.
Закон убывания предельного продукта в сильной форме:
![]() ,
, ![]() ,
,
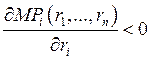 ,
, ![]() .
.
Упражнение Показать, что для функции Кобба-Дугласа выполняется закон убывания предельного продукта в сильной форме.
Средняя
отдача фактора ![]() (производительность i-го фактора):
(производительность i-го фактора):
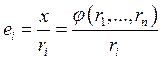 .
.
Максимум средней отдачи количества входного фактора соответствует точке пересечения графиков предельной производительности и средней отдачи. В точке предельной и средней производительности находится комбинация с минимальными издержками, отражающая оптимальное соотношение расхода фактора и выпуска продукции.
Теорема Если производственная функция однородна степени 1, то сумма предельных производительностей с весами в виде количества производственных факторов равна объёму выпуска:
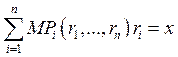
![]() ;
;
если производственная функция однородна степени ![]() , то
, то
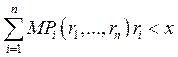
![]() ;
;
если производственная функция однородна степени ![]() , то
, то
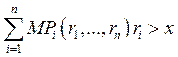
![]() .
.
►самостоятельно ◄
В неоклассической теории часто применяют различные виды эластичности.
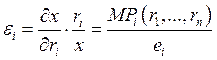 .
.
(![]() — для
— для ![]() -го
фактора).
-го
фактора).
Упражнение
Показать, что для функции Кобба-Дугласа ![]() .
.
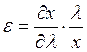 .
.
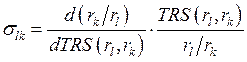 .
.
Упражнение Найти эластичность замещения для функции Кобба-Дугласа.
Упражнение Найти эластичность масштаба для функции Кобба-Дугласа.
Теорема Эластичность масштаба равна сумме эластичностей производства:
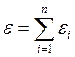 .
.
Одним из основных предположений неоклассической теории является линейная неоднородность производственной функции.
Теорема (о невозможности возрастающей отдачи)
Не существует
дифференцируемой производственной функции двух переменных ![]() , обладающей свойствами:
, обладающей свойствами:
![]() ;
;
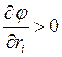 ,
, ![]() ;
;
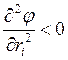
![]() ,
, ![]()
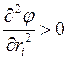
![]() ,
, ![]()
(т. е. меняется знак второй производной).
►без доказательства ◄
Лемма Имея две производственные функции с частичной вариацией факторов
![]() ,
, ![]()
![]() ,
, ![]()
можем всегда построить однородную производственную функцию, обладающую следующими свойствами:
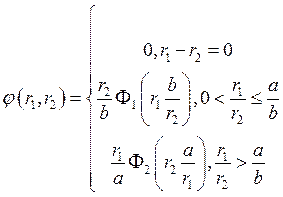
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.