Основы теории производства и издержек, страница 3

Благодаря замещаемости производственных факторов при использовании неоклассических производственных функций возможно один и тот же объём выпуска производить с использованием различных комбинаций входных факторов. Для выбора наилучшей комбинации обычно используют критерий минимума производственных издержек.

 — цены факторов,

.

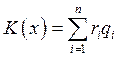Комбинация входных факторов, которая минимизирует издержки при производстве заданного выпуска называется комбинацией с минимальными издержками.

Лемма (о комбинации с минимальными издержками)

Комбинация с минимальными издержками удовлетворяет соотношению

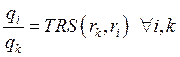, т. е. предельная норма замещения факторов равняется обратному отношению цен этих факторов.

►

       (*)

◄

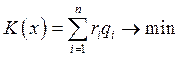
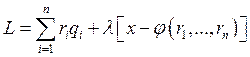
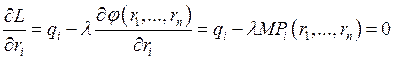
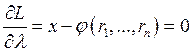
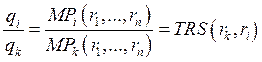Если мы наложим на производственную функцию ограничение: все изокванты должны быть выпуклыми (это более сильное утверждение; оно доказывается аналогично), то (*) является необходимым и достаточным условием комбинации с минимальными издержками.

Упражнение Интерпретация множителей Лагранжа.

,

Возьмём функцию Кобба-Дугласа. Для неё

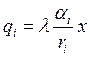
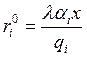
подставим последнее выражение в

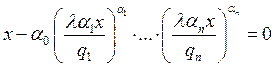
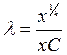
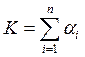
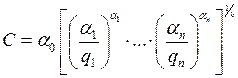
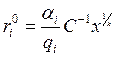
Заметим, что при , т. е. в случае постоянной отдачи от масштаба функция входных факторов линейна. В случае убывающего масштаба — вогнута.

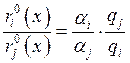, т. е., независимо от объёма выпуска —  — оптимальные по издержкам количества входных факторов находятся в постоянном соотношении друг с другом.

Это свойство справедливо для любой однородной производственной функции (а не только для функции Кобба-Дугласа). И его можно записать в виде следующей леммы:

Лемма (о линейной экспансии)

Для однородных производственных функций количества входных факторов с оптимальными издержками находятся в постоянном соотношении друг с другом независимо от объёма выпуска.

►без доказательства                                                                                                                   ◄

Лемма Для линейно однородных производственных функций функция издержек растёт линейно. Если производственная однородна степени , то функция издержек вогнута.

►без доказательства                                                                                                                   ◄

Модель межотраслевого баланса Леонтьева

Каждый продукт производится только в одной отрасли и каждая отрасль производит только один продукт.

Продукты, которыми выпускаются отраслями являются конечными продуктами, а могут также служить сырьём для производства других продуктов.

 — совокупный выпуск -ой отрасли за период.

 — количество продукции -ой отрасли, предназначенное для производства продукции, выпускаемой -ой отраслью (промежуточная продукция).

 — конечная продукция -ой отрасли.

, .

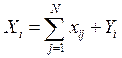Модель межотраслевого баланса принято записывать в виде таблицы межотраслевого баланса:

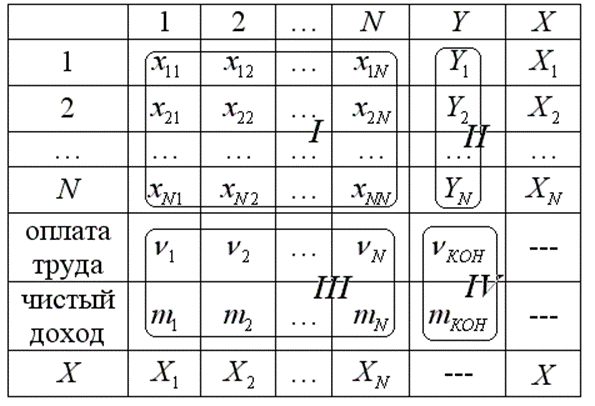
По столбцам идут потребляющие отрасли, по строкам — производящие, но отрасли одни и те же, каждая выступает в обеих ролях.

Смысл квадрантов:

• I —промежуточная часть производимой продукции, которая идёт в качестве текущих материальных затрат в другие отрасли;
• II — характеризует материально-вещественный состав конечного продукта (национального дохода);
• III — характеризует национальный доход со стороны стоимостного состава;
• IV — отражает конечное распределение национального дохода.

Стоимость продукции -ой отрасли, выходящей из области материального производства в сферу конечного потребления — .

Сумма по столбу должна равняться соответствующей сумме по строке.

Пример

Рассмотрим экономическую систему — необитаемый остров, где живёт Робинзон (один). Он потребляет в день 1 корзину еды и 3 охапки дров.

Охотясь целый день, он может добыть 10 корзин еды, собирая дрова — набрать 20 охапок дров, изготавливая орудия труда — сделать 5 каменных топоров (добывать дрова) или 10 бумерангов (для охоты).

За день Робинзон теряет/ломает 2 бумеранга и 1 топор.

Робинзон нуждается в отдыхе. После целого дня охоты ему нужно 0.25 дня отдыха, после заготовки дров — 0.5 дня, после изготовления орудий — 0.25 дня.

Построить межотраслевой баланс на 100 дней.