Основы теории производства и издержек

Основы теории производства и издержек

Производственные отношения — отношения между загрузкой производственных факторов и выпуском.

Функция издержек — отношение между количеством выпускаемой продукции и требуемым расходом производственных факторов.

Неоклассическая теория производства

Постулируется существование дважды непрерывно дифференцируемых функций со следующими свойствами:

• постоянная или убывающая эффективность при уменьшении масштабов производства;
• положительная, но убывающая предельная производительность при изменении одного фактора и постоянстве остальных;
• возможность замещения при невозрастающей продуктивной норме замещения.

Линейный анализ выпуска

• пропорциональность;
• аддитивность.

Выпуск  называется эффективным, не существует другого выпуска , обладающего следующими свойствами:

, , при этом  .

Вектор чистого выпуска эффективен тогда и только тогда, когда не существует другого вектора, которому соответствует большее количество какого-либо из конечных продуктов и при этом ни один из продуктов не производился бы в меньшем количестве и ни один из ресурсов не затрачивался бы в большем количестве.

, ,

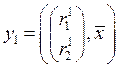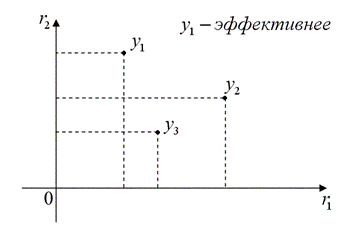
Множество всех возможных точек производства для данного набора факторов и продуктов — технология. Множество всех эффективных точек образует эффективную технологию.

Производственная функция

       

 — это отображение, которое каждой эффективной комбинации входных факторов ставит в соответствие число: количество выпускаемого продукта

.

В многомерном (несколько продуктов) случае в качестве производственной функции используют систему производственных отношений, которые удовлетворяют технически реализуемым комбинациям входных факторов

,

 .

Знание производственной функции позволяет:

• планирование производства — определение факторов;
• планирование ассортимента — определение комбинации конечных продуктов;
• планирование объёма выпуска конечной продукции.

Определение издержек

Издержки — это оценённая потребность товаров или услуг в производственных мощностях (входных факторах) для рассматриваемого периода.

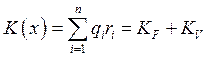, где  — фиксированные, а  — переменные издержки.

Два подхода к оцениванию стоимости средств производства

• закупочная цена;
• оппозиционные издержки (измеряется потерянная прибыль по сравнению с другими возможными вариантами загрузки).

Основная задача анализа издержек — это исследование зависимостей издержек от выпускаемого количества продукции при известной производственной функции.

Неоклассическая теория производства

Основное понятие в неоклассической теории производства — это производственная функция (отношение между входными и выходными факторами).

Множество всех вводимых комбинаций ресурсов и выпусков, которое охватывает технологически достижимые способы производства, называют технологией или производственным множеством.

,   

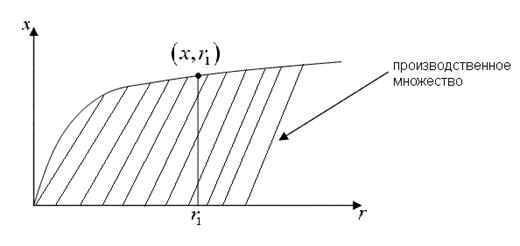
Точка  принадлежит производственному множеству, т. е., имея ресурс в количестве , мы можем произвести продукцию в объёме .

Обычно существование производственной функции постулируется:

Постулат: Существует отображение  пространства входных факторов в пространство выпуска, которое каждой комбинации входных факторов ставит в соответствие максимально возможное количество выходного (производимого) продукта

.

Замечание В дальнейшем, если не оговорено иное, будем рассматривать задачи, где есть всего 2 ресурса

.

Изокванта — это множество всех возможных комбинаций входных факторов, которых достаточно для производства данного объёма продукта. Рассмотрим несколько примеров построения изоквант.

Пример1

Студенты копают ямы лопатами (неэквивалентные ресурсы):

 — студенты,  — лопаты.

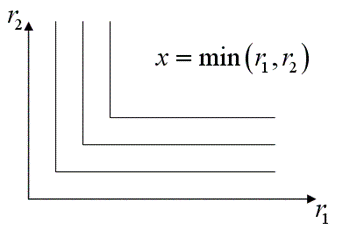
Пример2

Студенты пишут лекции ручками или карандашами (полностью взаимозаменяемые ресурсы):

 — ручки,  — карандаши.

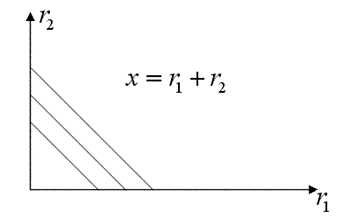
Пример3

Не полностью эквивалентные ресурсы.

Производственная функция Кобба-Дугласа

,

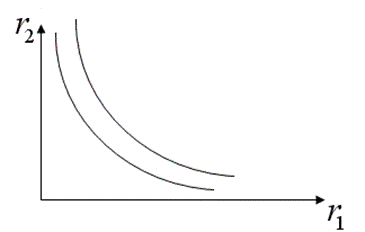
, ,  — константы:

 — измеряет масштаб производства,

,  — показывают, как меняется объём выпуска при изменении входных факторов.

Анализируются также вариации факторов.

1. Рассмотрим влияние вариации масштаба при постоянном соотношении количеств входных факторов.

Основной объект изучения — гомогенные (однородные) производственные функции.

, .                              (*)

Возможны варианты:

•  — возрастание эффективности выпуска (с ростом производства);
•  — постоянство выпуска;
•  — убывание (сокращение) эффективности выпуска.