Методы оптимизации.Методы решения транспортных задач линейного программирования

Цель работы:

Ознакомиться с методами решения транспортных задач линейного программирования: алгоритмами построения опорного плана, определением плана методом потенциалов.

Задание:

Решить исходную транспортную задачу методом потенциалов, определяя опорный план методом северо-западного угла и методом минимального  элемента.

По методу потенциалов сделать ручной просчет исходной транспортной задачи.

Постановка задачи линейного программирования:

Будем рассматривать нашу задачу как задачу линейного программирования в канонической форме, т.е.:

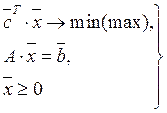. Перепишем исходную задачу в соответствии с рассмотренной формой. Поскольку необходимо выполнение условия:, то матрица А будет иметь 9 строк и 20 столбцов :

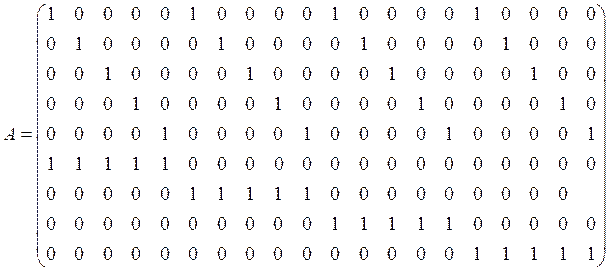
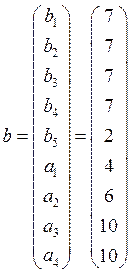
В итоге получается, что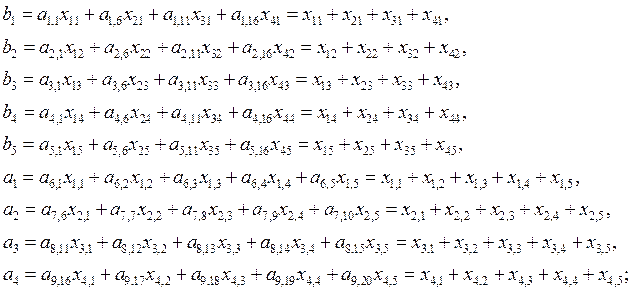

Таким образом, эта постановка задачи совпадает с транспортной.

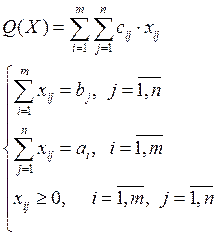
Построение опорного плана:

1.  Методом минимального элемента.

Затраты на перевозку по построенному плану:

2.  Методом северо-западного угла

Затраты на перевозку по построенному плану:

Решение задачи методом потенциалов с опорным планом, построенным методом минимального элемента:

1.  итерация

a)  система потенциалов

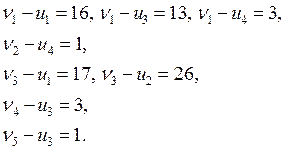
Отсюда получаем потенциалы:

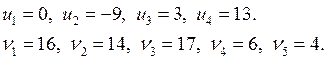
b)  проверяем систему на потенциальность

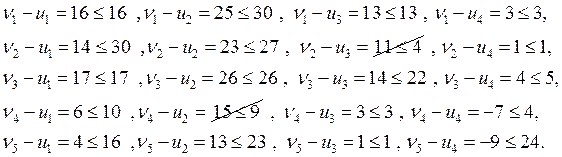
2.  итерация

a)  система потенциалов

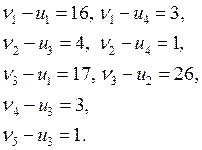
Отсюда получаем потенциалы:

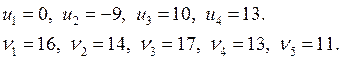
b)  проверяем систему на потенциальность

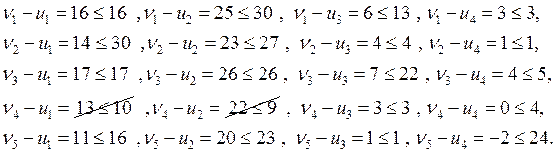
3.  итерация

a)  система потенциалов

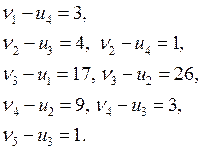
Отсюда получаем потенциалы:

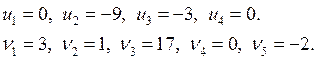
b)  проверяем систему на потенциальность

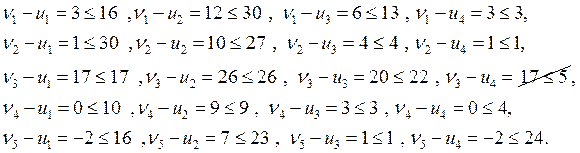
4.  итерация