Методы оптимизации.Методы решения транспортных задач линейного программирования, страница 3

Потенциалы:

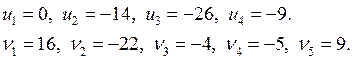
Ведущий элемент:

4.  итерация

ai        bj

7

7

7

7

2

4

4    16

0   30

0    17

0   10

0   16

6

3   30

0   27

0   26

3   9

2   23

10

0   13

7   4

1   22

0   3

0    1

10

0   3

0   1

6   5

4   4

0  24

Потенциалы:

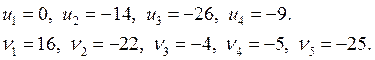
Ведущий элемент:

5.  итерация

ai        bj

7

7

7

7

2

4

4    16

0   30

0    17

0   10

0   16

6

2   30

0   27

0   26

4   9

0   23

10

1   13

7   4

0   22

0   3

2    1

10

0   3

0   1

7   5

3   4

0  24

Потенциалы:

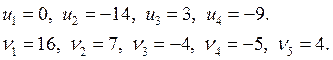
Ведущий элемент:

6.  итерация

ai        bj

7

7

7

7

2

4

4    16

0   30

0    17

0   10

0   16

6

0   30

0   27

0   26

6   9

0   23

10

1   13

7   4

0   22

0   3

2    1

10

2   3

0   1

7   5

1   4

0  24

Потенциалы:

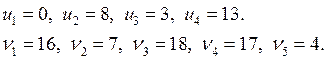
Ведущий элемент:

7.  итерация

ai        bj

7

7

7

7

2

4

4    16

0   30

0    17

0   10

0   16

6

0   30

0   27

0   26

6   9

0   23

10

0   13

7   4

0   22

1   3

2    1

10

3   3

0   1

7   5

0   4

0  24

Потенциалы:

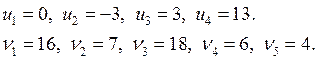
Ведущий элемент:

Транспортная задача вырождена.

Затем, получаем таблицу, рассмотренную ранее. При построении системы потенциалов и проверки на потенциальность получаем, что система потенциальна, значит, искомый план найден! 

За  7 итераций получаем тот же искомый план, что и в предыдущем случае:

Искомый план :

ai        bj

7

7

7

7

2

4

0   16

0   30

4    17

0   10

0   16

6

0   30

0   27

0   26

6   9

0   23

10

0   13

7   4

0   22

1   3

2    1

10

7   3

0   1

3   5

0   4

0   24

Затраты на перевозку по построенному плану:

Теперь решим задачу как задачу линейного программирования методом последовательного улучшения плана:

Скачать файл