Методы оптимизации.Методы решения транспортных задач линейного программирования, страница 2

Поскольку  , а количество элементов в таблице  равно 7, то задача вырождена.

a)  система потенциалов

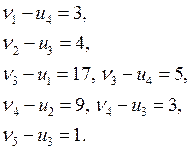
Поскольку система вырождена, то необходимо построить еще одно уравнение для системы. Выберем клетку для уравнения таким образом, чтобы  и из нее нельзя было построить цикл. В качестве такой клетки выберем , тогда дополнительное уравнений системы будет иметь вид:

Отсюда получаем потенциалы:

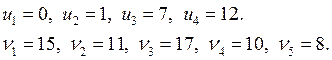
b)  проверяем систему на потенциальность

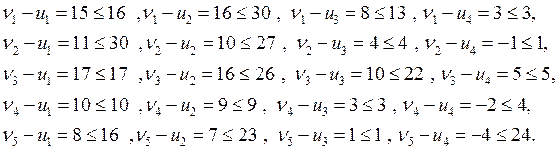
Полученная система потенциальна! Искомый план найден!

Искомый план :

ai        bj

7

7

7

7

2

4

0   16

0   30

4    17

0   10

0   16

6

0   30

0   27

0   26

6   9

0   23

10

0   13

7   4

0   22

1   3

2    1

10

7   3

0   1

3   5

0   4

0   24

Затраты на перевозку по построенному плану:

Аналогично можно решить задачу методом потенциалов с опорным планом, построенным по методу северо-западного угла.

A.  Опорный план

ai        bj

7

7

7

7

2

4

4    16

0   30

0    17

0   10

0   16

6

3   30

3   27

0   26

0   9

0   23

10

0   13

4   4

6   22

0   3

0    1

10

0   3

0   1

1   5

7   4

2   24

Затраты на перевозку по построенному плану:

B.  Метод потенциалов:

1. итерация

ai        bj

7

7

7

7

2

4

4    16

0   30

0    17

0   10

0   16

6

3   30

3   27

0   26

0   9

0   23

10

0   13

4   4

6   22

0   3

0    1

10

0   3

0   1

1   5

7   4

2  24

Потенциалы:

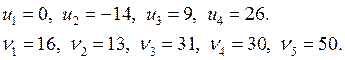
Ведущий элемент:

2.  итерация

ai        bj

7

7

7

7

2

4

4    16

0   30

0    17

0   10

0   16

6

3   30

1   27

0   26

0   9

2   23

10

0   13

6   4

4   22

0   3

0    1

10

0   3

0   1

3   5

7   4

0  24

Потенциалы:

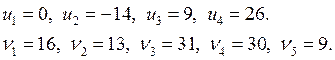
Ведущий элемент:

3.  итерация

ai        bj

7

7

7

7

2

4

4    16

0   30

0    17

0   10

0   16

6

3   30

0   27

0   26

1   9

2   23

10

0   13

7   4

3   22

0   3

0    1

10

0   3

0   1

4   5

6   4

0  24
Скачать файл