Информатика и выч. техника \ Моделирование систем и комплексов

Разработка программы для имитационного моделирования системы массового обслуживания с 6-ю устройствами, каждое из которых может одновременно обслуживать только одно требование

Страницы работы

6 страниц (Word-файл)

Скачать файл

Содержание работы

1.Анализ задачи и обзор аналогов.

1.1Анализ задачи

Требуется разработать программу для имитационного моделирования системы массового обслуживания с 6-ю устройствами, каждое из которых может одновременно обслуживать только одно требование. Интервалы времени между поступлением требований являются случайными независимыми величинами со средним значением. Время обслуживания является случайной величиной некоррелированной с интервалами поступления требований. Среднее значение времени обслуживания требований – 180 секунд. Если в момент поступления очередного требования имеется хотя бы одно свободное устройство, то оно немедленно приступает к обслуживанию этого требования, а если все обслуживающие устройства заняты и в очереди находится не более 14 требований, то реакция системы определяется дисциплиной обслуживания. Если же в очереди находятся 15 требований, то очередное требование покидает систему необслуженным. Оценке подлежат следующие параметры:

Коэффициент использования системы ;
Среднее время ожидания заявки в очереди ;
Среднее время пребывания заявки в системе ;
Среднее по времени число требований в очереди ;
Среднее по времени число требований в системе ;
Абсолютная пропускная способность ;
Относительная пропускная способность ;

Начальные значения параметров системы:

дисциплина обслуживания - циклическая с квантом q = 10 с;
количество устройств s = 6;
емкость накопителя l = 15;
среднее время поступления требований = 60 c;
среднее время обработки требований = 180 c.

Таким образом, задача сводится к имитационному моделированию системы массового обслуживания с шестью устройствами, работающую по циклическому механизму (без учета приоритетов) с отказами.

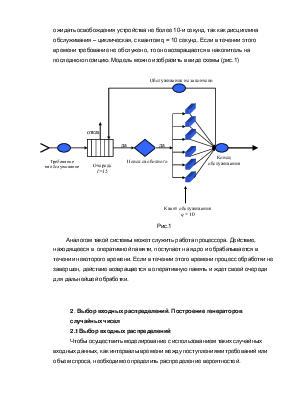
В системах с отказами, поступившее требование при наличии свободных устройств немедленно принимается к выполнению, в противном случае получает отказ. В нашем случае, требование, стоящее в очереди на первой позиции, будет ожидать освобождения устройства не более 10-и секунд, так как дисциплина обслуживания – циклическая, с квантом q = 10 секунд. Если в течении этого времени требование не обслужено, то оно возвращается в накопитель на последнюю позицию. Модель можно изобразить в виде схемы (рис.1)

Квант обслуживания q = 10

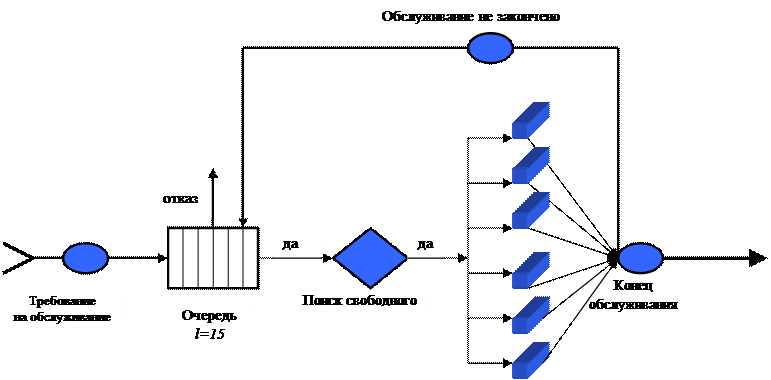Рис.1

Аналогом такой системы может служить работа процессора. Действие, находящееся в оперативной памяти, поступает на ядро и обрабатывается в течении некоторого времени. Если в течении этого времени процесс обработки не завершен, действие возвращается в оперативную память и ждет своей очереди для дальнейшей обработки.

2. Выбор входных распределений. Построение генераторов случайных чисел

2.1 Выбор входных распределений

Чтобы осуществить моделирование с использованием таких случайных входных данных, как интервалы времени между поступлениями требований или объем спроса, необходимо определить распределение вероятностей.

Для определения распределения вероятностей поступления заявок необходимо произвести некоторые логические выкладки. Анализируя техническое задание можно сделать вывод, что события поступления заявок не коррелируют друг с другом, т. е. вероятность поступления одной заявки не влияет на вероятность поступления другой заявки. А следовательно, поток заявок представляет собой распределение с отсутствием последействия. Поступление заявки возможно в произвольный момент времени, а следовательно появление заявок — непрерывная случайная величина. Единственное распределение, обладающее описанными свойствами — экспоненциальное.

Экспоненциальное распределение

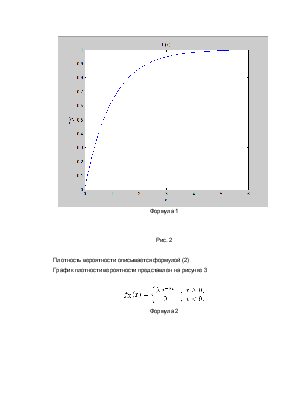
Функция распределения описывается формулой (1)

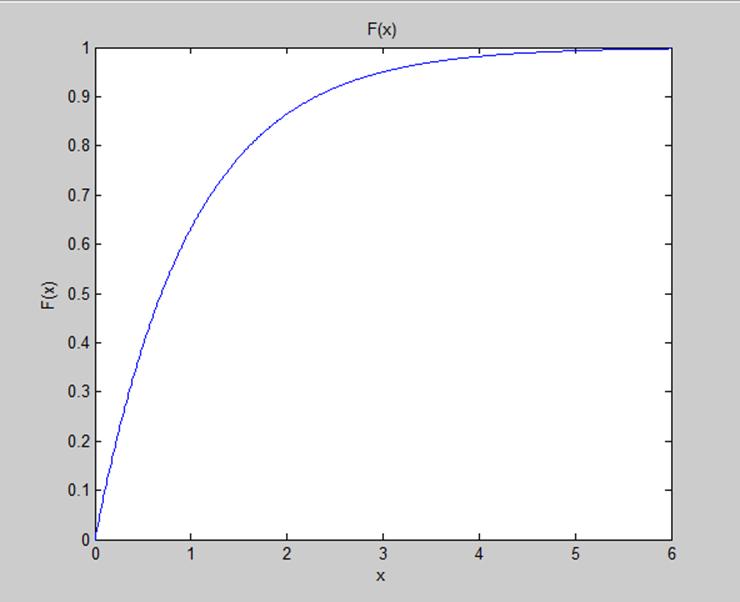
График функции распределения представлен на рисунке 2

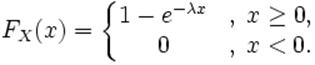
$F_X(x) = \left\{\begin{matrix} 1-e^{-\lambda x}&,\; x \ge 0, \\ 0 &,\; x < 0. \end{matrix}\right.$

Формула 1

Рис. 2

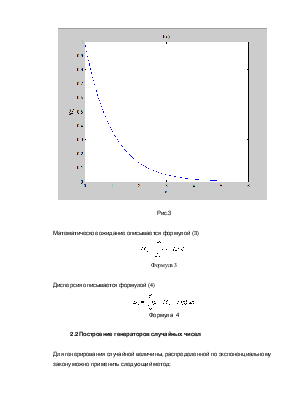
Плотность вероятности описывается формулой (2)

График плотности вероятности представлен на рисунке 3

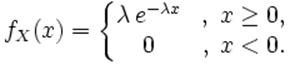
$f_X(x) = \left\{\begin{matrix} \lambda \,e^{-\lambda x} &,\; x \ge 0, \\ 0 &,\; x < 0. \end{matrix}\right.$

Формула 2

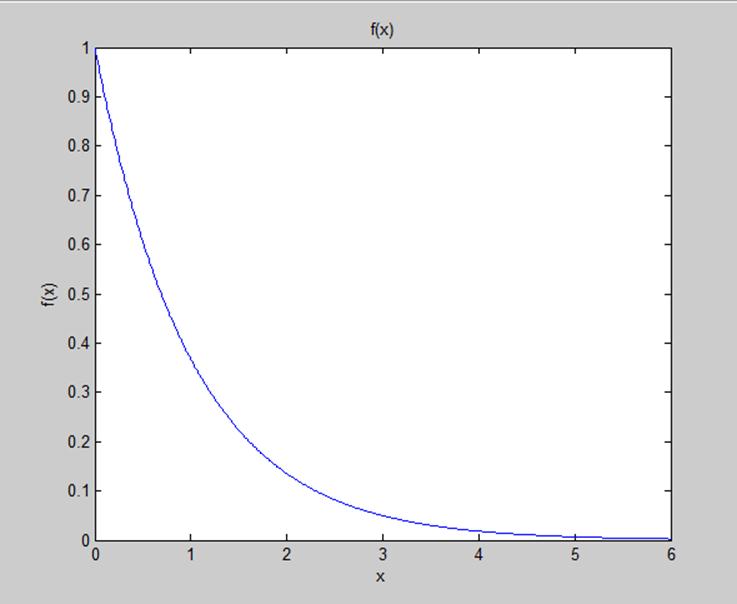
Рис.3

Математическое ожидание описывается формулой (3)

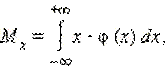
Формула 3

Дисперсия описывается формулой (4)

Формула 4

2.2 Построение генераторов случайных чисел

Для генерирования случайной величины, распределенной по экспоненциальному закону можно применить следующий метод:

— С помощью мультипликативного генератора генерируется последовательность, представляющей собой значения стандартно равномерно распределенной случайной величины, представленной на формуле (5)

xi+1 = (axi) (mod m),

xiÎ(1, m-1), |(1, m-1)|=m-1

Формула 5

m = 231- 1 = 2 147 483 647

a = 630 360 016