Определение устойчивости дискретной САУ (параметры системы: K = 10, T1 = 3.0, T2 = 1.0, T3 = 0.1, T0 = 0.2)

БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ "ВОЕНМЕХ"

им. Д. Ф. УСТИНОВА

Домашняя задание №2

по учебной дисциплине

                             Теория автоматического управления____                                      _ 

на тему

                         Определение устойчивости дискретной САУ                                                                        

студента                    _Будюхиной Надежды Андреевны ___________ _________           ___н

Фамилия,        Имя,           Отчество

группа    И362      н

САНКТ-ПЕТЕРБУРГ

2009 г.

Задание: система регулирования имеет в своем контуре цифровую вычислительную машину (ЦВМ). Структурная схема системы:

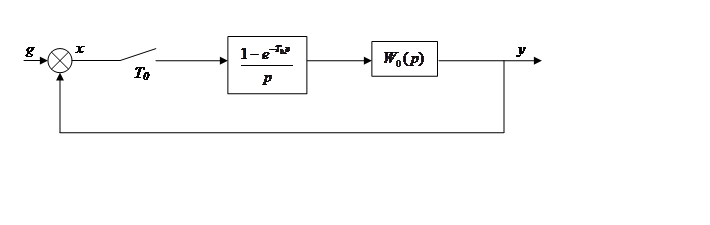
Найти z – передаточные функции разомкнутой  и замкнутой  системы в предположении, что запаздывание в ЦВМ отсутствует и можно пренебречь влиянием квантования по уровню, т.е. можно рассматривать линейную задачу. Проверить устойчивость САУ  c помощью критерия Гурвица и критерия Найквиста с использованием логарифмических псевдочастотных характеристик. Рассчитать и представить в виде графика переходную характеристику системы.

Вариант 3.5:

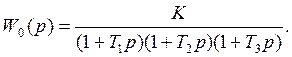
Параметры системы: K = 10, T₁ = 3.0, T₂ = 1.0, T₃ = 0.1,  T₀ = 0.2.

1. Нахождение передаточной функции разомкнутой системы.

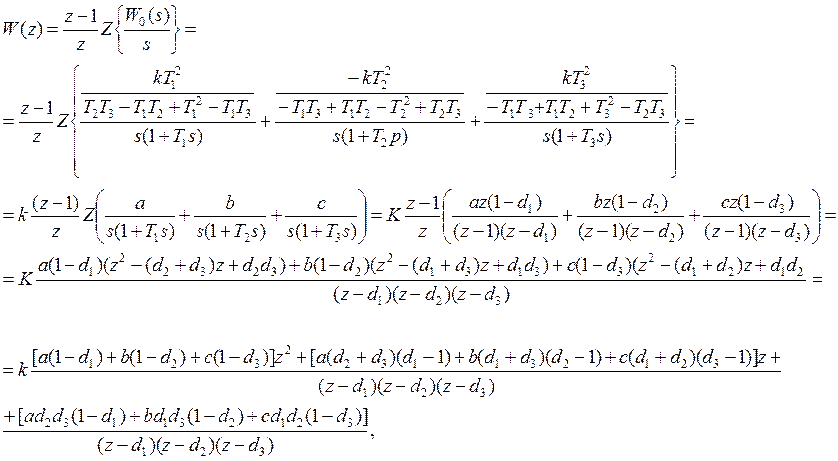
где d₁ = exp(-T₀/T₁) = 0.93 0.92                                

d₂ = exp(-T₀/T₂) = 0.82  0.88

d₃ = exp(-T₀/T₃)  = 0.13 0.14

 ~~~~

 ~~~~~~~

 ~~~~~~~~~

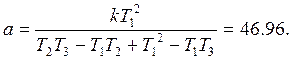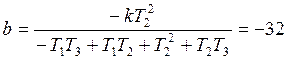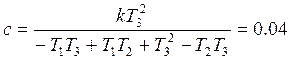С учётом числовых значений, получим:

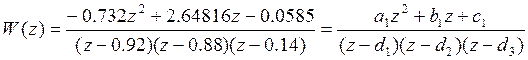
2. Нахождение передаточной функции замкнутой системы.

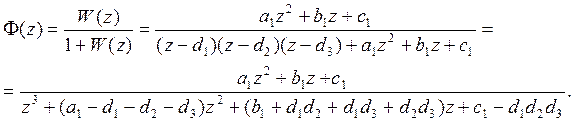
Подставим числовые значения:

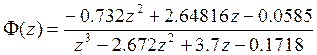
3. Анализ устойчивости.

Критерий Гурвица.

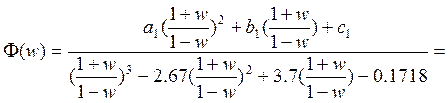
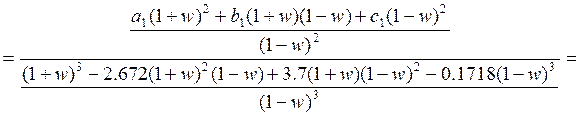
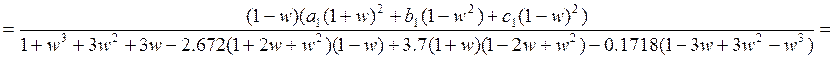
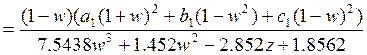
Для данного характеристического полинома можно использовать критерий Гурвица. Для устойчивости системы необходимо, чтобы все определители Гурвица были положительны. Найдём определители:

1.452(-2.852) – 7.5438 1.8562 < 0

Второй определитель Гурвица отрицательный, следовательно, система не является устойчивой.

Критерий Найквиста.

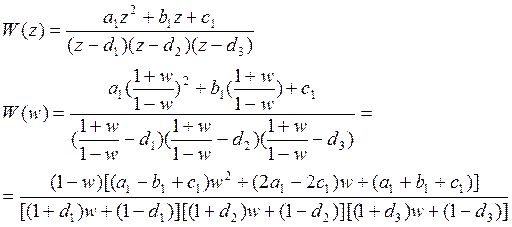
Подставим числовые значения:

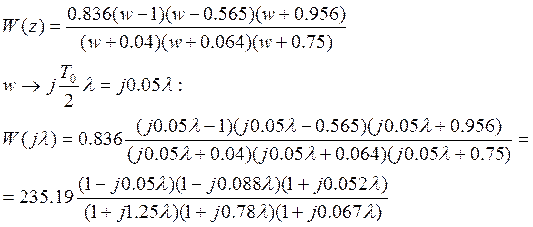
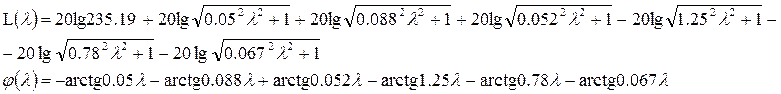
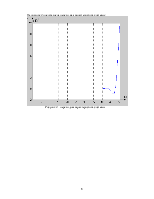
На рисунке 1 представлены логарифмические псевдочастотные характеристики.

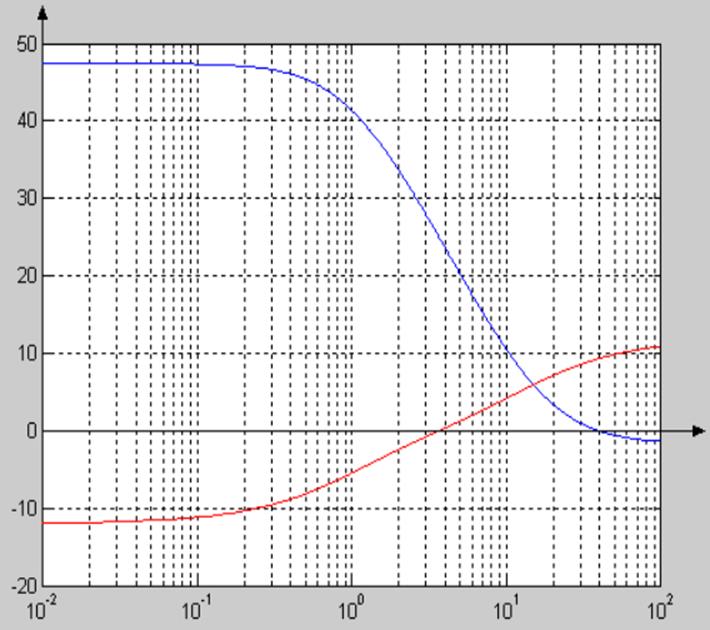
Рисунок 1 – логарифмические псевдочастотные характеристики

Используя логарифмические псевдочастотные характеристики можно сделать вывод о неустойчивости системы.

На рисунке 2 представлена переходная характеристика системы:

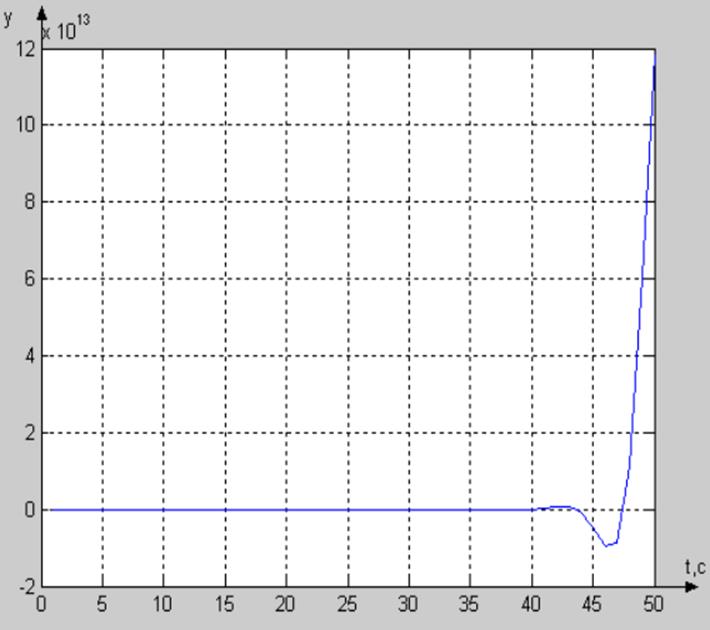
Рисунок 2 – переходная характеристика системы