






1 Постановка задачи
Схема № 1, вариант № 3.
Система регулирования имеет в своем контуре цифровую вычислительную машину (ЦВМ). Блок-схема системы с ЦВМ и эквивалентная структурная схема приводятся на рисунках 1 и 2 соответственно.
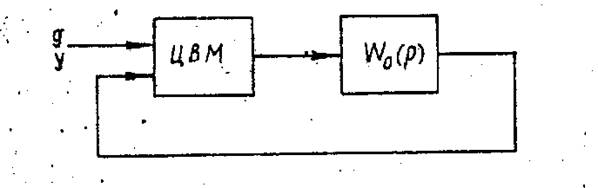
Рисунок 1 – Блок-схема системы регулирования с ЦВМ
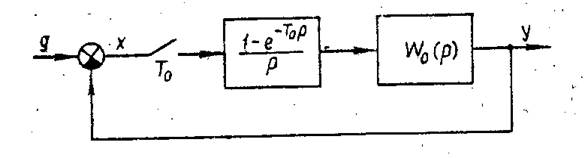
Рисунок 2 – Эквивалентная структурная схема системы регулирования с ЦВМ
Найти ![]() -передаточные функции
разомкнутой
-передаточные функции
разомкнутой ![]() и замкнутой
и замкнутой ![]() системы
в предположении, что запаздывание в ЦВМ отсутствует и можно пренебречь влиянием
квантования по уровню, т.е. можно рассматривать линейную задачу. Проверить
устойчивость СУ с помощью алгебраического критерия Гурвица и с помощью критерии
Найквиста с использованием логарифмических псевдочастотных характеристик.
системы
в предположении, что запаздывание в ЦВМ отсутствует и можно пренебречь влиянием
квантования по уровню, т.е. можно рассматривать линейную задачу. Проверить
устойчивость СУ с помощью алгебраического критерия Гурвица и с помощью критерии
Найквиста с использованием логарифмических псевдочастотных характеристик.
Рассчитать и представить в виде графика переходную характеристику системы.
Передаточная функция непрерывной части
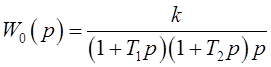 .
.
Численные
значения коэффициентов: общий коэффициент усиления ![]() , постоянные
времени
, постоянные
времени ![]() ,
, ![]() , период
дискретности ЦВМ
, период
дискретности ЦВМ ![]() .
.
2 Построение переходной характеристики
2.1 Передаточные функции системы
Передаточная
функция ![]() разомкнутой системы может быть найдена согласно
[3]:
разомкнутой системы может быть найдена согласно
[3]:
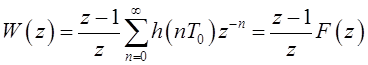 , (1)
, (1)
где
![]() − переходная функция непрерывной части в
дискретные моменты времени
− переходная функция непрерывной части в
дискретные моменты времени ![]() , а
, а ![]() представляет собой
представляет собой ![]() -преобразование
этой функции.
-преобразование
этой функции.
Поскольку
переходная функция ![]() является преобразованием Лапласа
от передаточной функции непрерывной части
является преобразованием Лапласа
от передаточной функции непрерывной части ![]() ,
деленной на
,
деленной на ![]() , т.е.
, т.е.
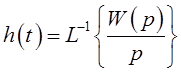 , то часто используют
символическую запись формулы (1)
, то часто используют
символическую запись формулы (1)
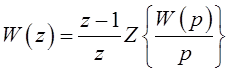 .
.
При этом дискретная передаточная функция может определяться в следующей последовательности:
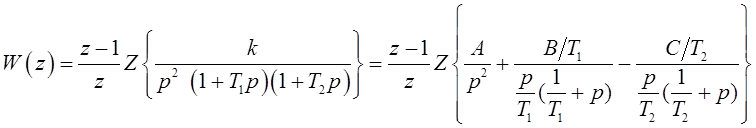 ,(2)
,(2)
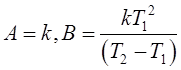 ,
, 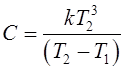 .
.
![]() -преобразование каждого
слагаемого в правой части (2) нетрудно определить, воспользовавшись таблицей
-преобразование каждого
слагаемого в правой части (2) нетрудно определить, воспользовавшись таблицей ![]() -преобразования [1, 3],
-преобразования [1, 3],
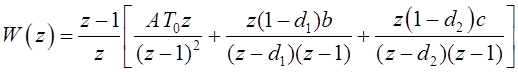 ,
,
![]() ,
, ![]() .
.
Окончательное выражение или
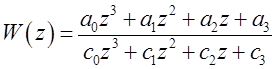 .
.
Подстановка численных значений дает
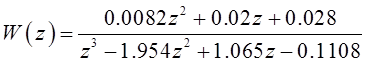 . (3)
. (3)
Передаточная функция замкнутой системы
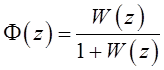 ,
,
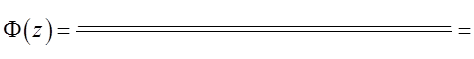
или
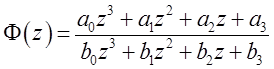 .
.
Подстановка численных значений дает
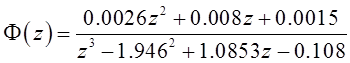 . (4)
. (4)
2.2 Переходная характеристика замкнутой дискретной системы
Перепишем выражение для передаточной функции (4):
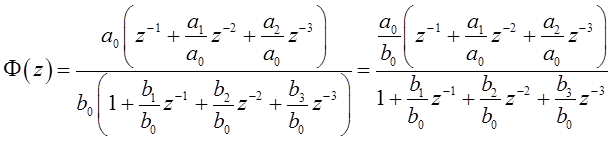 . (5)
. (5)
Передаточной функции (5) соответствует уравнение в обратных разностях
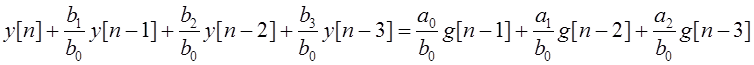 ,
,
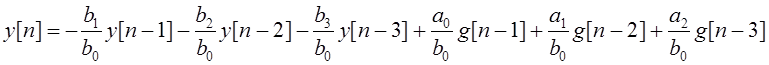 где
где ![]() −
переходная функция замкнутой системы в дискретные моменты времени
−
переходная функция замкнутой системы в дискретные моменты времени ![]() ,
,
![]() − задающее воздействие в виде единичного
постоянного сигнала.
− задающее воздействие в виде единичного
постоянного сигнала.
График переходной характеристики изображен на рисунке 3.
Переходная характеристика, интерполированная кубическими сплайнами Эрмита, изображена на рисунке 4.
Программа построения переходной характеристики приведена в приложении А.
3 Определение устойчивости дискретной САУ
3.1 Устойчивость по алгебраическому критерию Гурвица
3.1.1
Использование критерия для исследования устойчивости
дискретных систем
Чтобы применить критерий устойчивости Рауса-Гурвица к
дискретной системе , произведем замену переменной, введя новую переменную ![]() подстановкой:
подстановкой:
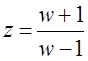 . (6)
. (6)
Области устойчивости в виде круга радиуса 1 в
плоскости ![]() (или полосы шириной
(или полосы шириной ![]() левее мнимой оси в плоскости
левее мнимой оси в плоскости ![]() ) соответствует вся левая полуплоскость
комплексной плоскости новой переменной
) соответствует вся левая полуплоскость
комплексной плоскости новой переменной ![]() .
Границей устойчивости при этом является вся мнимая ось: изменению
.
Границей устойчивости при этом является вся мнимая ось: изменению ![]() на
на ![]() соответствует
изменение
соответствует
изменение ![]() от
от ![]() до
до ![]() . Таким образом, в результате такой
подстановки получается уравнение (передаточная функция), условия устойчивости
для которого совпадают с условиями устойчивости непрерывных систем. Поэтому к
нему непосредственно могут быть применены все известные для непрерывных систем
критерии устойчивости. Для применения критерия Рауса-Гурвица надо использовать
знаменатель
. Таким образом, в результате такой
подстановки получается уравнение (передаточная функция), условия устойчивости
для которого совпадают с условиями устойчивости непрерывных систем. Поэтому к
нему непосредственно могут быть применены все известные для непрерывных систем
критерии устойчивости. Для применения критерия Рауса-Гурвица надо использовать
знаменатель ![]() передаточной функции (4) системы.
передаточной функции (4) системы.
3.1.2 Составление определителей Гурвица
У системы
![]() .
.
После подстановки сюда выражения (6) получаем
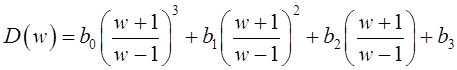 .
.
Раскрытие скобок и отбрасывание знаменателя дает
![]()
Подставив численные значения, получаем
![]() . (7)
. (7)
Коэффициенты полинома (7) положительны, необходимое условие устойчивости системы выполнено.
Второй определитель Гурвица
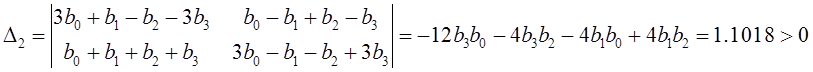 .
.
Определитель положителен, следовательно, система устойчива
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.