Анализ особых точек и построение фазовых портретов линейных систем

Практическое занятие 7.Анализ особых точек и построение фазовых портретов линейных систем.

Пример 1.

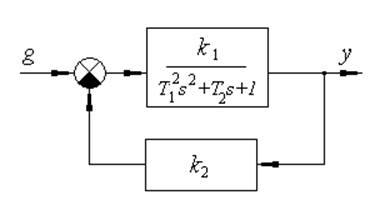
Исходные данные: k₁=5;  k₂=0,8;  T₁²=1;  T₂=6;  g(t)=1(t).

Найти и классифицировать особые точки на фазовой плоскости. Построить примерный фазовый портрет системы.

Перейдем к модели в форме системы дифференциальных уравнений:

,

.

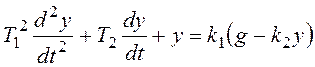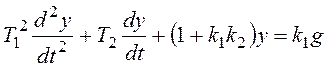Отсутствие производных входного сигнала в правой части уравнения позволяет ввести фазовые переменные наиболее удобным для построения фазового портрета образом: x₁=y, . В результате получим:

,

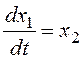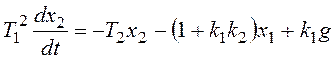
или

.

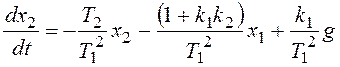Подставим в уравнения числовые данные:

,

.

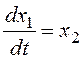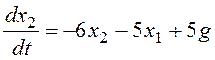Рассчитаем координаты особой точки (у линейной системы особая точка возможна только одна):

,

,  .

Составим матрицу А и найдем ее собственные числа:

,

,

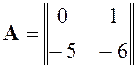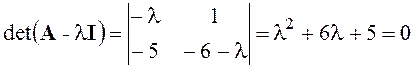l₁=-1,   l₂=-5.

Вывод: для рассматриваемой системы на фазовой плоскости имеется одна особая точка с координатами (1; 0) – устойчивый узел.

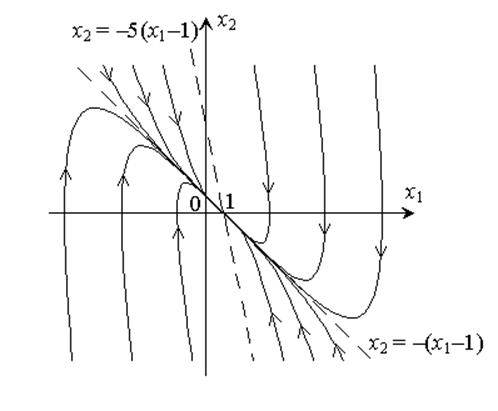
Для рассматриваемого базиса собственные числа матрицы А определяют наклон особых линий на фазовой плоскости. Особые линии – прямые x₂ = –(x₁–1) (касательная к фазовым траекториям в особой точке) и x₂ = –5(x₁–1).

Примерный фазовый портрет показан на рисунке.

Пример 2.

Модель задана в форме системы уравнений:

,

.

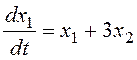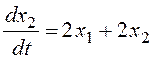Найти и классифицировать особые точки на фазовой плоскости. Построить примерный фазовый портрет системы.

Рассчитаем координаты особой точки:

,

.

Такая система имеет «тривиальное» решение:

, .

Найдем собственные числа матрицы А:

,

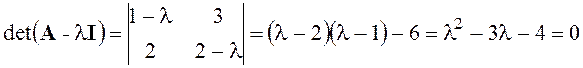l₁=-1,   l₂=4.

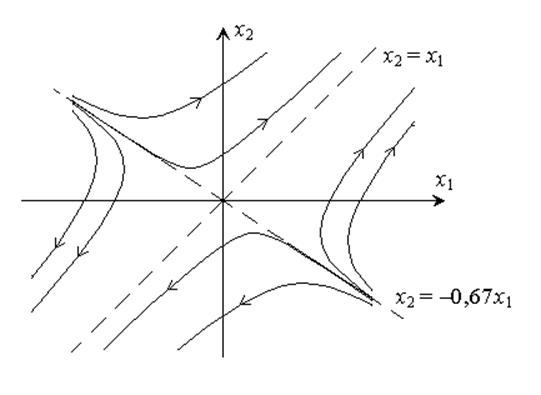
Вывод: для рассматриваемой системы на фазовой плоскости имеется одна особая точка с координатами (0; 0) – седло.

Фазовые траектории – гиперболы. Особые линии – асимптоты гипербол. Их наклоны найдем из уравнения

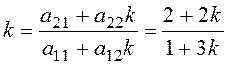
или

,

3k² – k – 2 = 0,

k₁=1,  k₂= –0,67.

Особые линии на фазовой плоскости – прямые x₂ = x₁ и x₂ = –0,67x₁.

Для определения направления движения по фазовым траекториям найдем значения составляющих вектора скорости движения, например, в точке (0; 1):

,

.

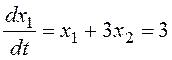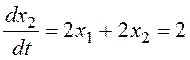Вектор скорости в рассмотренной точке направлен вправо и вверх.

Примерный фазовый портрет показан на рисунке.

Пример 3.

Исходные данные: k=5;  T₁=0,2;  T₂=1;  g(t)=10.1(t).

Найти и классифицировать особые точки на фазовой плоскости. Построить примерный фазовый портрет системы.

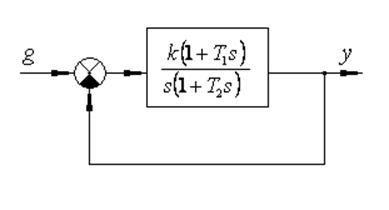
Запишем общее дифференциальное уравнение системы

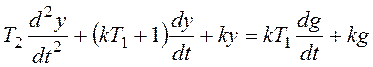
и перейдем к модели в форме системы дифференциальных уравнений:

,

,

,

,

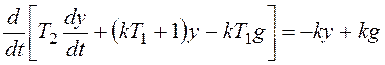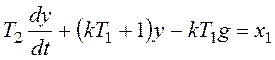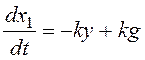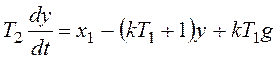y=x₂;

в итоге:

,

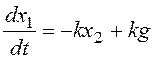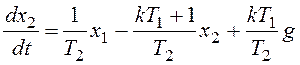, или в числах:

,

.

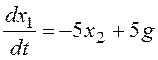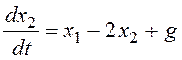Рассчитаем координаты особой точки:

,

;

,

.

Найдем собственные числа матрицы А:

,

.

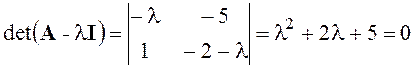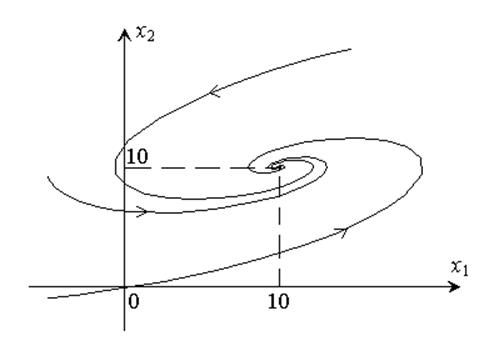
Вывод: для рассматриваемой системы на фазовой плоскости имеется одна особая точка с координатами (10; 10) – устойчивый фокус.

Фазовые траектории – сходящиеся в особую точку спирали. Направление движения по фазовым траекториям определим, рассчитав составляющие вектора скорости движения изображающей точки, например, в начале координат:

,

.

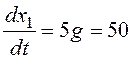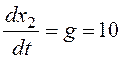Таким образом, если ось x₁ выбирается в качестве горизонтальной, направление движения по фазовым траекториям – против часовой стрелки.