



Практическое занятие 9. Расчет процессов в дискретных системах
Пример 1. Рассчитать процесс в системе, описываемой разностным уравнением
4x[n+2]+4x[n+1]-3x[n]=g[n]
при g[n]=0 и начальных условиях x[0]=8, x[1]=-6.
Воспользуемся классическим методом.
Составим характеристическое уравнение: 4z2+4z-3=0 и найдем его корни:
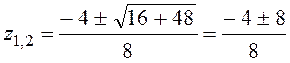 ,
,
z1=0,5; z2=-1,5.
В результате общее решение имеет вид:
![]() .
.
Найдем произвольные постоянные:
x[0]=C1+C2=8,
x[1]=0,5C1-1,5C2=-6;
C2=8-C1,
0,5C1-12+1,5C1=-6,
2C1=6,
C1=3, С2=5.
В результате:
![]() .
.
Рассчитаем процесс на нескольких тактах (x[0] и x[1] известны):
![]() ,
,
![]() ,
,
![]() и так далее.
и так далее.
Теперь на основе заданного уравнения составим рекуррентную формулу:
4x[n+2]=-4x[n+1]+3x[n],
x[n]=-x[n-1]+0,75x[n-2]
и рассчитаем процесс на нескольких тактах:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() и так далее.
и так далее.
Пример 2. Рассчитать процесс в системе, описываемой разностным уравнением
x[n+3]-3x[n+2]+3x[n+1]-x[n]=g[n]
при g[n]=0 и начальных условиях x[0]=1, x[1]=4, x[2]=9.
Воспользуемся классическим методом.
Составим характеристическое уравнение: z3-3z2+3z-1=0 и найдем его корни:
(z-1)3=0.
Уравнение имеет один вещественный корень z=1 кратности k=3.
В результате общее решение имеет вид:
![]() .
.
Найдем произвольные постоянные:
x[0]=C1=1,
x[1]=C1+C2+C3=4,
x[2]=C1+2C2+4C3=9;
1+C2+C3=4,
C3=3-C2,
1+2C2+4C3=9,
2C2+12-4C2=8,
4=2C2,
C2=2, С3=1.
В результате:
![]() .
.
Рассчитаем процесс на нескольких тактах (x[0], x[1] и x[2] известны):
![]() ,
,
![]() ,
,
![]() ,
,
![]() и так далее.
и так далее.
Пример 3. Найти реакцию системы, описываемой разностным уравнением
6x[n+2]-5x[n+1]+x[n]=g[n]
при g[n]=1 и нулевых начальных условиях x[0]=x[1]=0.
Составим рекуррентную формулу:
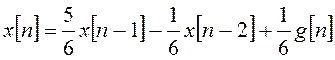
и рассчитаем процесс на нескольких тактах:
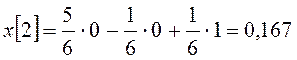 ,
,
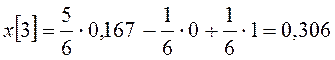 ,
,
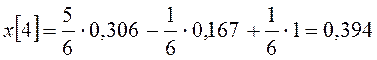 ,
,
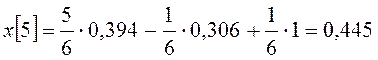 и так далее.
и так далее.
Теперь воспользуемся классическим методом.
Составим характеристическое уравнение: 6z2-5z+1=0 и найдем его корни:
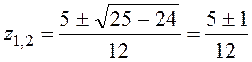 ,
,
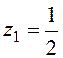 ,
, 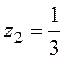 .
.
В результате общее решение имеет вид:
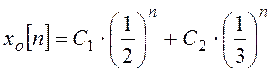 .
.
Частное решение ищут в форме, соответствующей функции в правой части уравнения. При g[n]=const ищем x*[n]=a:
6a-5a+a=1,
2a=1,
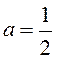 .
.
Таким образом, полное решение имеет вид:
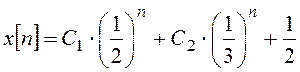 .
.
Найдем произвольные постоянные:
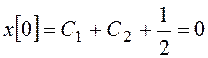 ,
,
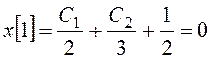 ;
;
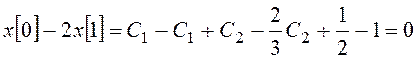 ,
,
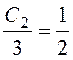 ,
,
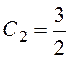 ,
,
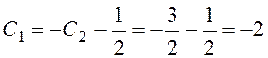 .
.
В результате:
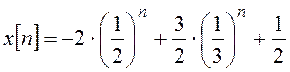 .
.
Рассчитаем процесс на нескольких тактах:
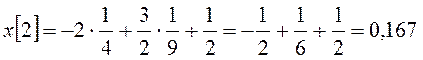 ,
,
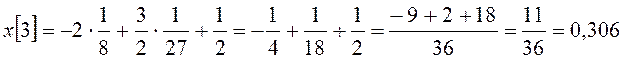 ,
,
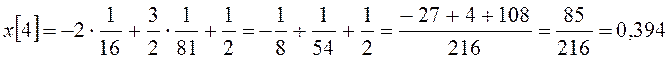
и так далее.
Решим задачу операторным методом.
Разностному уравнению соответствует дискретная передаточная функция дискретной системы:
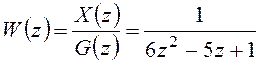 .
.
Учтем изображение заданного входного сигнала 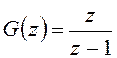 и получим изображение искомого сигнала
x[n]:
и получим изображение искомого сигнала
x[n]:
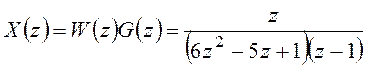 .
.
Преобразуем эту дробь в сумму табличных изображений:
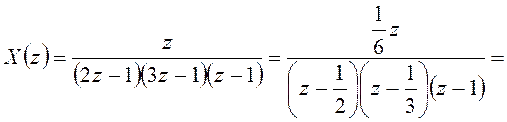
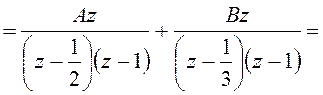
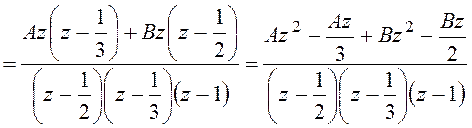 ;
;
A+B=0,
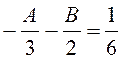 ;
;
B=-A,
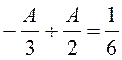 ,
,
A=1, B=-1;
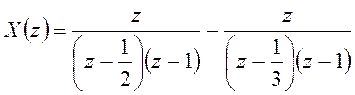 .
.
Теперь учтем, что для решетчатой функции ![]() , или
, или ![]() ,
где
,
где ![]() , z-изображение имеет вид
, z-изображение имеет вид 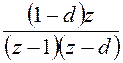 :
:
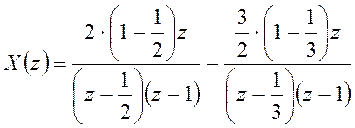 .
.
Запишем искомую решетчатую функцию:
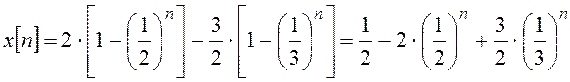 , что
совпадает с полученным выше результатом.
, что
совпадает с полученным выше результатом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.