Image1.Canvas.Rectangle(j*round((x-36)/10)+39,y-round(y1/(slych1/y))-39,(j+1)*round((x-36)/10)+38,y-38);
Image1.Canvas.Brush.Color:=RGB(255,255,255);
s:=FloatToStr(Conv1(y1,3));
Image1.Canvas.TextOut(j*round((x-36)/10)+36+round(x/20),y-round(y1*y/slych1)-55,s);
s:=FloatToStr(Conv1(min,3));
Image1.Canvas.TextOut(j*round((x-36)/10)+9,y-15,s);
Image1.Canvas.MoveTo(31,y-round(y*(j+1)/10)-39);
Image1.Canvas.LineTo(35,y-round(y*(j+1)/10)-39);
s:=FloatToStr(Conv1(((j+1)*slych1/10),3));
Image1.Canvas.TextOut(3,y-round(y*(j+1)/10)-45,s);
y1:=0;
min:=min+(max+0.001)/10;
end;
end;
procedure TForm1.ChislocChange(Sender: TObject);
begin
c:=round(exp((Chisloc.Position+1)*ln(2)));
s:=FloatToStr(c);
Label1.Caption:=s;
end;
procedure TForm1.ChislobChange(Sender: TObject);
begin
case Chislob.Position of
0:b:=1;
1:b:=3;
2:b:=5;
3:b:=7;
4:b:=11;
5:b:=13;
6:b:=17;
7:b:=19;
8:b:=23;
9:b:=29;
10:b:=31;
end;
s:=FloatToStr(b);
Label2.Caption:=s;
end;
procedure TForm1.ChislokChange(Sender: TObject);
begin
case Chislok.Position of
0:k:=1;
1:k:=3;
2:k:=5;
3:k:=7;
4:k:=11;
5:k:=13;
6:k:=17;
7:k:=19;
8:k:=23;
9:k:=29;
10:k:=31;
end;
s:=FloatToStr(k);
Label3.Caption:=s;
end;
procedure TForm1.ChislomChange(Sender: TObject);
begin
m:=Chislom.Position*10/100+80;
s:=FloatToStr(m);
Label4.Caption:=s;
end;
function TForm1.Conv1(A: Double; n: integer): Double;
begin
Result:=int(A*power(10,n))/power(10,n);
end;
procedure TForm1.FormActivate(Sender: TObject);
begin
s:=FloatToStr(c);
Label1.Caption:=s;
s:=FloatToStr(b);
Label2.Caption:=s;
s:=FloatToStr(m);
Label4.Caption:=s;
s:=FloatToStr(k);
Label3.Caption:=s;
s:=FloatToStr(slych1);
Label5.Caption:=s;
end;
procedure TForm1.ChislosChange(Sender: TObject);
begin
slych1:=Chislos.Position*100;
s:=FloatToStr(slych1);
Label5.Caption:=s;
end;
end.
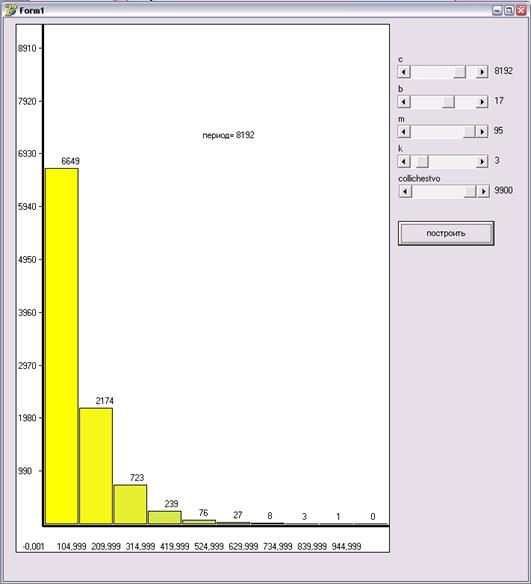
Рис. 1.6. Результаты работы программы
1.4. Описание лабораторной работы № 1
1. Разработать процедуру, которая генерирует последовательность псевдослучайных чисел с заданным законом распределения.
2. Написать программу, которая получает максимальное число псевдослучайных чисел, и строит гистограмму распределения полученных псевдослучайных чисел.
3. Оценить математическое ожидание и дисперсию полученных псевдослучайный чисел.
4. Вычислить период генератора псевдослучайных чисел.
Варианты заданий:
1. Равномерное распределение (a=5;b=30).
2. Треугольное распределение (a=3;d=8,b=13).
3. Нормальное распределение ( m=-1; s=1).
4. Экспоненциальное распределение (m=0,5)
5. Распределение Пуассона (m=1)
6. Распределение Эрланга (m=1;k=4).
7. Логнормальное распределение (m=0;s=0,1).
8. Гамма - раcпределение (a=0,5;b=1).
9. Бета - распределение (a=1,5;b=5).
10. Равномерное распределение ( a=-1;b=25).
11. Треугольное распределение (a=20;d=25,b=30).
12. Нормальное распределение ( m=10; s=1).
13. Экспоненциальное распределение (m=1)
14. Распределение Пуассона (m=2)
15. Распределение Эрланга (m=2;k=2).
16. Логнормальное распределение (m=1;s=1).
17. Гамма - раcпределение (a=3,5 ;b=1/3).
18. Бета - распределение (a=2,5 ;b=2).
19. Равномерное распределение ( a=50;b=128).
20. Треугольное распределение (a=50;d=75;b=128).
21. Нормальное распределение ( m=1; s=2).
22. Экспоненциальное распределение (m=4,5)
23. Распределение Пуассона (m=4)
24. Распределение Эрланга (m=4,2;k=5).
25. Логнормальное распределение (m=0,3;s=1).
26. Гамма - распределение (a=3,7;b=0,2).
27. Бета - распределение (a=5,5;b=5).
28. Равномерное распределение (a=-20;b=-1).
29. Треугольное распределение (a=-20;d=-15,b=0).
30. Нормальное распределение (m=5; s=0,1).
31. Экспоненциальное распределение (m=7)
32. Распределение Пуассона (m=8)
33. Распределение Эрланга (m=7;k=6).
34. Логнормальное распределение (m=0,3;s=1).
35. Гамма - распределение (a=1,5;b=1).
36. Бета - распределение (a=2,7;b=1).
37. Равномерное распределение (a=100;b=1000).
38. Треугольное распределение (a=100;d=500,b=10000).
39. Нормальное распределение (m=100; s=20).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.