Сборник задач и упражнений по курсу "Моделирование" (Мультипликативный конгруэнтный генератор с простым модулем)

Мультипликативный конгруэнтный генератор с простым модулем

Для мультипликативных конгруэнтных генераторов период, равный (c-1), может быть получен, если с=2^n-1, a-простой корень с (а является простым корнем с, если а^c-1=1+c*k, где k - целое, и для любого целого q<c-1 выражение (a*q-1)/с не является целым).

Равномерное распределение в интервале от [a;b]

x=a+ (b-a)*r, где r -  равномерно распределено в интервале [0;1].

Треугольное распределение в интервале от [a;b] с модой d

x = a + sqrt ((d-a)*(b-a)*r)  для 0 <=r<= (d-a)* (b-a)

x = b – sqrt ((b-d)*(b-a)*(1-r)) для  (d-a)*(b-a) <r<= 1, где r равномерно распределено в интервале [0;1].

Нормальное распределение с математическим ожиданием m

и дисперсией  s

Нормальные выборки генерируются парами. Пусть a = 2*r₁-1 и b=2*r₂-1, где r₁ и r₂ – независимые псевдослучайные числа, равномерно распределенные в интервале от [0,1]. 

Пусть w = a*a+b*b. Если w>1.0, повторить процедуру, если  w<=1.0, тогда x₁= (a*sqrt(-2.0*ln(w)/w))*m+s,  x₂ =(b*sqrt(-2.0*ln(w)/w))*m+s.

Экспоненциальное распределение с математическим ожиданием m

x=-m*ln(r),где r равномерно распределено в интервале [0;1].

Распределение Пуассона с математическим ожиданием m

Установить значение выборки x равным первому значению n, такому что

 _{n                   n+1}

П ri >= e^-m > П ri

                                                                     ^{i=1                            i=1}

где ri равномерно распределено в интервале [0;1].

Распределение Эрланга

Распределение Эрланга есть сумма k экспоненциально одинаково распределенных случайных величин с математическим ожиданием m.

_k            

x = - m.*ln(П ri),

     ⁱ⁼¹

где ri равномерно распределено в интервале [0;1].

Логнормальное распределение

В уравнение L=eⁿ подставляется значение выборки n из нормального распределения:

x=e^y, где y - нормально распределенная случайная величина с математическим ожиданием m и дисперсией  s.

Гамма-распределение

Метод получения выборки из гамма-распределения является функцией параметра a. Эффективность метода растет с увеличением значения a.

Если  a - целое число, то необходимо применять распределение Эрланга при k=a и    m=b.

а). 0<a<1

Пусть x=r₁^(1/a)     и   y=r₂^(1/(1-a)). Если x+y<=1, вычислить w=x/(x+y). В противном случае пересчитать значения x и y.

Случайное число равно w*(-ln(r₃))*b.  

r₁,r₂,r₃ - случайные числа, равномерно распределенные в интервале [0;1].

б). 1<a<5

Пусть a - целая часть a, b - дробная часть a.

_a

Вычислить x=(a/a)*(-ln(Пr_i)). Если r_a+1>(x/a)^b*exp(-b*(x/(a-1))),

ⁱ⁼¹

пересчитать x . В противном случае случайное число равно x*b.

в).  a>5

Если r₁>= a-a , то необходимо применять распределение Эрланга с параметрами k=a и m=b.

Если r₁< a-a , то необходимо применять распределение Эрланга с параметрами k=aa+1  и m=b.

Бета-распределение

Случайное число равно g1/(g1+g2), где g1  и g2 - случайные числа, гамма-распределенные со следующими параметрами:

g1 - a=a ; b=1

g2 - a=b ; b=1

1.2. Оценка математического ожидания и дисперсии

псевдослучайных чисел

При построении оценок параметров  по данным выборки необходимо рассматривать два различных случая.

В первом случае выборка содержит только значения самих наблюдений без учета моментов времени осуществления этих наблюдений. Примером такой выборки могут служить данные о времени ожидания обслуживания посетителями. Статистики по независимой от времени выборке называются статистиками по наблюдениям или точечными статистиками.

Во втором случае значения случайных величин определены во времени. Например, число занятых кассиров в магазине является случайной величиной, значение которой меняется во времени. При этом нас интересует информация о том, какие значения принимала наблюдаемая случайная величина и на каких интервалах времени. Статистики по зависимой от времени выборке называются временными или интервальными статистиками.

Таблица 1.1. Формулы для вычислений среднего и дисперсии по выборке

В табл.1.1 приведены формулы для вычисления как точечных, так и интервальных статистик  и . Для интервального случая выборочное среднее обозначается , где Т равно общей продолжительности интервала времени наблюдения. Для вычисления  существует несколько формул, однако приводимая здесь формула наиболее удобна с вычислительной точки зрения. Отметим, что для вычисления точечных статистик необходимо знать значения и размер выборки I. Аналогично для вычисления интервальных оценок необходимо знать 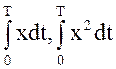 и Т.

1.3. Программная реализация генерации псевдослучайных чисел

Задание

1.  Разработать процедуру, которая генерирует последовательность псевдослучайных чисел, равномерно распределенных на интервале (5;30).