Сборник задач и упражнений по курсу "Моделирование" (Мультипликативный конгруэнтный генератор с простым модулем), страница 2

2.  Написать программу, которая получает максимальное число псевдослучайных чисел, и строит гистограмму распределения полученных псевдослучайных чисел.

3.  Оценить математическое ожидание и дисперсию полученных псевдослучайный чисел.

4.  Вычислить период генератора  псевдослучайных чисел.

Математическое решение задачи

1.  Чтобы получить последовательность псевдослучайных чисел, равномерно распределенных на интервале [0;1], применяем конгруэнтный метод, использующий следующее рекурсивное уравнение:

z _i=(a*z_i-1+b) (mod c), i=1,2,3,...,

r_i=z_i/ (c-1), где z₀ - базовое число, а r_i является i-м псевдослучайным числом, b - простое число относительно c, a=4*k+1, где  k -  целое.

2.  Чтобы получить последовательность псевдослучайных чисел, равномерно распределенных на интервале [5;30] из имеющейся последовательности из п.1, используем формула:

x=a+ (b-a)*r, где r -  равномерно распределено в интервале [0;1], a=5,b=30.

3.  Чтобы получить гистограмму распределения, разобьем отрезок [5;30] на 10 равных отрезков и подсчитаем количество чисел, попавших в каждый из этих отрезков, и на основании полученных данных построим гистограмму распределения.

4.  Для вычисления математического ожидания  используем формулу:

5. 

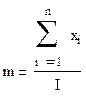
где m – математическое ожидание, I – размер выборки.

Для чисел, равномерно распределенных на интервале [a;b], математическое ожидание вычисляется по формуле:   m=(a+b)/2. Подставив в данное выражение значения a=5, b=30, получим m=(5+30)/2=17.5.

Для вычисления дисперсии псевдослучайных чисел воспользуемся формулой:

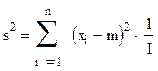, где s^2 – дисперсия.

Для чисел, равномерно распределенных на интервале [a;b], дисперсия вычисляется по формуле:  s^2=[(b-a)^2]/12. Подставив в данное выражение значения a=5, b=30, имеем: s^2=[(30-5)^2]/12 ~ 52.08333.)

5.  Для вычисления периода генератора будем сравнивать первое число последовательности с последующими до обнаружения совпадения; период будет равен разности индексов повторяющихся членов последовательности. В данном конгруэнтном генераторе период будет максимален и равен c=2^n, где n- разрядность компьютера, если b- простое число относительно с.

Программа

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, TeEngine, Series, ExtCtrls, TeeProcs, Chart, StdCtrls, ComCtrls;

type

TForm1 = class(TForm)

Chart1: TChart;

Button1: TButton;

Series1: TAreaSeries;

Button2: TButton;

Period: TLabel;

m_o: TLabel;

dispersiya: TLabel;

Bevel1: TBevel;

Button3: TButton;

Button4: TButton;

procedure Button1Click(Sender: TObject);

procedure Button2Click(Sender: TObject);

procedure Button3Click(Sender: TObject);

procedure Button4Click(Sender: TObject);

private

{ Private declarations }

function  Chislo():Single;

procedure Raspredelenie(Sender: TObject);

public

{ Public declarations }

end;

const

A1=5;    {Границы распределения}

B1=30;

N=65536; {Размерность массива псевдослучайных чисел}

var

Form1: TForm1;

k:integer=5;  {Параметры генератора псевдослучайных чисел}

b:integer=7;

z:integer=3;

c:integer=65536;

T:integer;    {Период генератора}

m: single;    {Математическое ожидание}

s: single;    {Дисперсия}

x:array[1..N]of Single; {Массив из N псевдослучайных чисел}

y:array[1..11]of integer;

FLAG: bool=false;

f:bool=true;

implementation

{$R *.dfm}

uses Unit2, Unit3;

{Функция получения числа, равномерно распределенного на отрезке [5;30]}

function TForm1.Chislo():Single;

var

a: integer;

r: single;

begin

a:=4*k+1;

z:=(a*z+b)mod c;

r:=z/(c-1);           {числo, равномерно распределенноe на отрезке [0;1]}

result:=A1+(B1-A1)*r; {числo, равномерно распределенноe на отрезке [5;30]}

end;

{Процедура получения N равномерно распределенных на интервале [5;30] псевдослучайных чисел}

procedure TForm1.Raspredelenie(Sender: TObject);

var

sum:single;

i: integer;

flag:bool;

begin

flag:=false;

for i:= 1 to N do

begin