Термоэлектронная эмиссия. Экспериментальная проверка закона Ричардсона-Дешмана: Методические указания к лабораторному практикуму, страница 3

Формулу  Ричардсона-Дешмана принято записывать в следующем модифицированном виде  [8]:

J=A(1-g) Т²exr (-W/kТ)=А^'Т² exr(-W/kТ),                                                                                                                        (7)

где g - коэффициент отражения Шоттки (g£1)

Например, для чистого вольфрама имеем: g=0,5. Поэтому для этого металла результаты, полученные по формулам (2) и (7), практически совпадают. Однако для других металлов они будут разными. Во всех других случаях следует пользоваться формулой (7).

Величина коэффициента g, к сожалению, сильно зависит от многих факторов. Среди них – физическое состояние поверхности металла; степень его химической чистоты и т.п. Например, упомянутый выше вольфрам иногда (по технологическим причинам) легируют очень небольшим количеством (<1%) тория. При столь малых концентрациях тория, казалось бы, не следует ожидать существенного изменения эмиссионной способности катода. В действительности же эмиссия электронов с такого катода резко возрастает. Причину удалось установить только после выполнения специальных исследований. Оказалось, что металлический торий при высоких температурах постепенно диффундирует на поверхность вольфрама и при хорошем вакууме образует там мономолекулярный слой атомов тория. Работа выхода у такого слоя меньше, чем у чистого вольфрама и чистого тория (в монолите): 2,63 эВ, 4,54 эВ и 3,30 эВ соответственно. Опыты показали, что средняя эффективность эмиссии торированного вольфрама примерно на порядок выше аналогичной эффективности чистого вольфрама.

Поскольку в реальных металлах всегда имеются различные примеси, а их поверхности не могут быть абсолютно чистыми, наблюдается большой разброс полученных в эксперименте численных значений эмиссионных постоянных, входящих в формулу (7). По этой причине  экспериментальной проверке подлежит лишь общая математическая структура этой формулы. Проще всего это сделать путем приведения закона Ричардсона-Дешмана (7) к безразмерному виду, выбирая для каждого исследуемого металла свои индивидуальные нормировочные  параметры, определяемые эмиссионными постоянными (А' и W). В итоге мы получим следующую универсальную формулу, одинаковую для всех чистых металлов:

у = х² exp(-х^-1),                                                  (8)

В эту формулу входит безразмерная температура х=Т/Т_о, где Т_о=W/k ,                                                                                                                                                                   (9)

и безразмерная поверхностная плотность тока эмиссии у = J ¤ J _о ,  где J _о=А' Т²_о .                                                                                                                                                            (10)

Из элементарного анализа формулы (8) следует, что ключевую роль в зависимости тока эмиссии от температуры играет экспоненциальный множитель. Действительно, дифференцируя (8), находим, что относительное изменение тока эмиссии, вызванное изменением температуры, определяется выражением

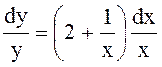,                                                                                                                                                                 (11)                                            

где первое слагаемое в скобке определяет вклад в  dy/yпервого сомножителя, а второе  слагаемое – второго сомножителя в (8).

Видно, что доминирующая роль экспоненциального множителя в (8) будет во всех случаях, когда:

2х<<1 .                                                                                                                                                                        (12)

Например, для вольфрама, у которого

W/е=4,54 эВ;    А=0,60∙10⁶А/м²K²; g=0,5 ,                                                                                                                                         (13)