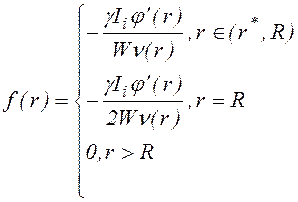Анализ движения заряженных частиц в разрядах с осциллирующими электронами, страница 8

                                          (1.3.8)

при заданной функции j(r). Если j(r) заранее неизвестно, то для расчета характеристик разряда необходимо cовмеcтное решение  кинетичеcкого  уравнения и уравнения Пуаccона для ионного слоя.

Изложенная выше методика может быть использована для расчета вольт-амперной характеристики разряда в условиях когда уход электронов в продольном направлении не является существенным. Однако при пониженных давлениях, когда Р близко к Р_cr, пренебрегать уходом быстрых частиц из разряда нельзя. Если движение частиц как в радиальном, так и в продольном направлении происходит в кнудсеновском режиме, то для оценки ухода быстрых частиц из разряда можно использовать известное из кинетической теории газов выражение для числа ударов частиц об стенку , где  - средняя скорость быстрых частиц, которую, учитывая, что скорость быстрой частицы меняется от  до 0, можно положить равной .

Если режим движения не является кнудсеновским (длина пробега l много меньше длины рассматриваемой области L), то оценить уход быстрых частиц можно используя диффузионное приближение, причем для коэффициента диффузии быстрых частиц можно использовать следующее соотношение

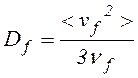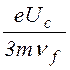=.                                                     (1.3.9)

При записи этого соотношения учтено что квадрат скорости быстрой частицы меняется от  до 0 и в среднем составляет величину порядка . Введенное обозначение  это эффективная частота столкновений быстрых электронов. В характерном для быстрых частиц диапазоне энергий транспортное сечение также как и ионизационное с приемлемой для оценочных расчетов точностью можно аппроксимировать зависимостью вида , что позволяет считать эффективную частоту константой.

В рассматриваемом случае (l<<L) переносом быстрых частиц в результате дрейфа, происходящего под влиянием слабого электрического поля, имеющегося в плазме, можно пренебречь по сравнению с переносом вследствие диффузии. Чтобы убедиться в этом, оценим отношение расстояния l, на которое частица переместится за время релаксации в результате дрейфа, к характерной диффузионной длине l_D. Для времени релаксации быстрых частиц можно записать следующее соотношение

t_r = 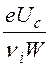,                                                                             (1.3.10)

а среднюю напряженность электрического поля оценить как

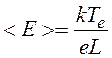,                                                                          (1.3.11)

где Т_е - температура плазменных электронов. Тогда для искомого отношения получаем

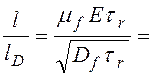
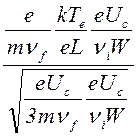.                                          (1.3.12)

Проведя сокращения и учитывая, что ионизационная и эффективная частоты для быстрых электронов являются величинами того же порядка, что и эффективная частота для плазменных электронов n_е, и используя известное соотношение

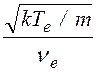 ~  ~                                                            (1.3.13)

можно преобразовать (1.3.12 ) к следующему виду

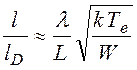<<1,                                                               (1.3.14)

что и требовалось доказать.

Выводы

Изложена методика расчета распределений медленных  частиц, находящихся  в  потенциальной яме, основанная на раздельном рассмотрении уходящих и захваченных частиц, причем расчет функции  распределения  захваченных частиц проводится на основе последовательного анализа релаксации частиц по энергии и свободных колебаний. Получено интегральное уравнение, учитывающее возможный  уход  захваченных  частиц  в продольном направлении, и рассмотрены возможности его  упрощения в различных предельных случаях.

Получены кинетические уравнения в энергетическом и амплитудном пространствах для быстрых частиц, испытывающих  неупругие столкновения. Рассмотрены возможности упрощенного учета ухода быстрых частиц в продольном направлении.

Результаты проведенного анализа будут использованы в следующих главах для расчета характеристик  тлеющего разряда с осциллирующими электронами.