Анализ движения заряженных частиц в разрядах с осциллирующими электронами, страница 3

f(x,v_x) = f_os(x,v_x) + f_es(x,v_x),                                              (1.1.6)

где  f_os   и  f_es   - соответственно функции распределения захваченных (осциллирующих) и уходящих частиц. При сделанном допущении интеграл столкновений зависит только от вида функции f_os и уравнение  (1.1.4)  распадается на два уравнения для функций f_os   и  f_es

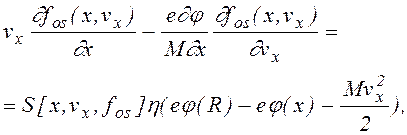                      (1.1.7)

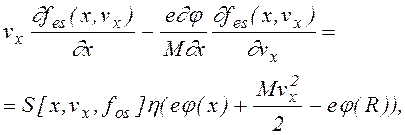                      (1.1.8)

где h(y) = 1, при  y > 0  и h(y) = 0, при  y < 0.

Уравнение   (1.1.7) можно подвергнуть дальнейшему упрощению при использовании следующего подхода. Из выполнения условия  (3.5)  следует, что  характерная частота столкновений n много меньше частоты колебаний в потенциальной яме n_os,  поскольку n ~ <v> / l,  а n_os ~ <v> / R, т.е. большую часть времени частицы совершают свободные колебания. Столкновения, при которых меняется энергия частицы и,  соответственно,   амплитуда  колебаний a   (переход   к   амплитуде     e = ej(a)  возможен при  соблюдении  симметрии, j(x) = j(-x),  что обычно выполняется), редки, и поэтому нахождение распределения  f_os(x,v_x) можно разбить на  два  этапа, сначала рассмотреть сравнительно медленный процесс  релаксации частиц по энергии  или  амплитуде, определить  соответствующую функцию распределения   f(a) , а затем выразить   f_os(x,v_x)   через f(a), считая, что частицы совершают  свободные  колебания. Для функции, зависящей от амплитуды, левая часть  (1.1.7)  oбращается в 0 и  (1.1.7)  принимает вид

S[a,j(a)] h(ej(a))=0.                                    (1.1.9)

В работе  [83]  проведена подробная процедура  преобразования кинетического уравнения в фазовом  пространстве  к  уравнению  в  пространстве интегралов  движения. В  настоящей  работе  связь между  f_os(x,v_x) и f(a) и интегральное уравнение для f(a) получим непосредственно из физических соображений.

Частица,  находясь в точке х, будет иметь скорость в промежутке  v_x ¸ v_x +dv_x в том случае, если ее амплитуда находится в промежутке  a¸  a + da, где  a, da  связаны с v_x, dv_x   следующими соотношениями

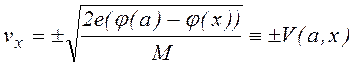,                           (1.1.10)

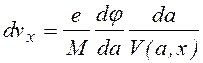.                                                      (1.1.11)

Относительное время нахождения такой частицы в промежутке  dx

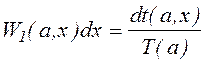,            при ½x½< a,                    (1.1.12)

где  dt(a,x)=dx/V(a,x), а T(a)=4 - период колебаний. Таким образом, для числа частиц в элементе  dxdv_x  фазового  пространства получаем соотношение

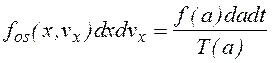.                                           (1.1.13)

Подставляя в  (1.1.13)  соотношения  (1.1.10), (1.1.11), получим

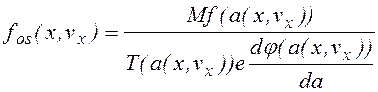,                         (1.1.14)

где  a(x,v_x) = j^-1(j(x) + Mv_x²/2e), j^-1  - функция, обратная к j(x). Интегрируя  f_os(x,v_x) по всем возможным скоростям, получим распределение по поперечной координате

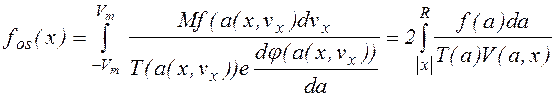,     (1.1.15)

где  V_m = V(R,x) = V(a,x)_a=R .

Уменьшение числа частиц в интервале  a ¸ a + da  происходит  за счет столкновений и равно n(a)f(a)da, где n(a) - усредненная по периоду колебаний частота столкновений. Новые частицы  появляются как за счет столкновений, в результате  которых  частица, имевшая амплитуду  a', попадает в промежуток  a ¸  a + da, так  и  за счет ионизации. В общем виде интегральное уравнение можно  записать следующим образом

-n(a)f(a) + G(a)+òW(a,a¢)f(a¢)n(a¢)da¢ = 0,                (1.1.16)

где G(a) - распределение частиц, образующихся в единицу времени в результате  ионизации,  W(a,a') - плотность  вероятности  для частицы, имевшей амплитуду  a',  приобрести в результате столкновения амплитуду a.  Отметим, что , т.к. есть вероятность получeния частицей в  результате  столкновения  энергии, достаточной для преодоления потенциального  барьера. Образование новых частиц происходит, как правило, при ионизации  электронным ударом и определяется параметрами распределения быстрых электронов. Принимая, что в момент появления частицы имеют максвелловское распределение по скоростям, для G_i(a) получаем следующее выражение