Общая методика анализа характеристик ансамбля большого числа частиц, находящихся в потенциальной яме, при низких давлениях предложена в [83] и заключается в составлении кинетического уравнения в пространстве интегралов невозмущенного столкновениями движения. Такой подход реализован в [83] для описания стабилизированного электронного пучка, но без учета условий образования и ухода частиц. Наличие этих процессов и соблюдение баланса между ними является принципиальным условием существования устойчивых газоразрядных структур. С учетом этого обстоятельства изложенная в [83] методика будет применена в настоящей главе для описания ансамбля частиц в условиях, характерных для газовых разрядов низкого давления. В 1.1 анализируется колебательное движение медленных частиц, испытывающих лишь упругие столкновения. Полученное кинетическое уравнение уточняется в 1.2 с учетом продольного движения частиц. В 1.3 анализируется колебательное движение быстрых частиц, для которых характерны неупругие столкновения.
1.1 Кинетическое уравнение в амплитудном пространстве для осциллирующих медленных частиц.
Обычно в разрядах низкого давления потенциал плазмы выше потенциала любого из электродов и большая часть электронов заперта в потенциальной яме. Вместе с тем, как уже отмечалась выше, возможна и противоположная ситуация, когда запертыми в потенциальной яме оказываются ионы. Такая ситуация реализуется в разрядах низкого давления в магнитном поле, например в Пеннинговских разрядах [4], а также при прохождении электронного пучка через остаточный газ [84]. Для последнего случая известны две модели, рассматривающие различные предельные ситуации.
В модели [85] предполагается, что причиной ухода ионов из области пучка является осевой градиент электрического поля и распределение плотности ионного заряда в продольном направлении определяется формулой
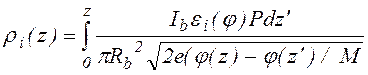, (1.1.1)
где Ib -ток пучка, ei - коэффициент ионизации, Р - давление газа, Rb - радиус пучка, e - заряд электрона j - потенциал, М - масса иона. Уравнение (1.1.1) справедливо в том случае, когда продольная составляющая электрического поля значительно превосходит поперечную состовляющую [84]. Поперечный ионный профиль будет в этом случае близок к профилю электронного пучка (в [85] распределение по поперечной координате принималось равномерным).
В работе [86] для поперечного профиля используется функция Больцмана
,
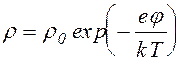(1.1.2)
где k - постоянная Больцмана, Т - температура газа. Такая ситуация возможна при незначительной скорости ухода частиц из области пучка как в продольном, так и в поперечном направлении, когда глубина ямы отвечает условию
.
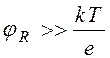(1.1.3)
В общем случае (1.1.3) не выполняется, и поперечное распределение может существенно отличаться от Больцмановского. Для его нахождения необходимо решение кинетического уравнения, которое в плоской геометрии в стационарном случае имеет следующий вид
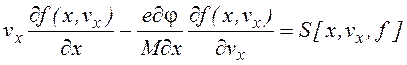(1.1.4)
с граничными условиями f(R,vx) = 0, при vx < 0, f(-R,vx) = 0, при vx < 0 (если в расматриваемую область частицы извне не попадают), где S- интеграл столкновений, x, vx - поперечные координата и скорость.
При выполнении условия низкого давления
l >> R, (1.1.5)
кинетическое уравнение можно существенно упростить. Частица, образовавшаяся в точке x со скоростью vx, удовлетворяющей условию Mvx2 / 2 > ej(R) - ej(x), с большой вероятностью уйдет из потенциальной ямы, т.к. при выполнении условия (1.1.5) вероятность столкновения на пути от точки образования до края ямы пренебрежимо мала и , таким образом, можно принять, что вклад в интеграл столкновений внесут только захваченые частицы, для которых Mvx2 / 2 < ej(R) - ej(x). Представим функцию распределения в виде суммы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.