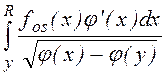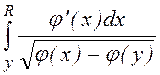
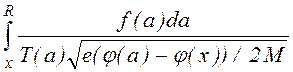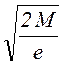
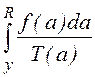
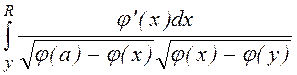Анализ движения заряженных частиц в разрядах с осциллирующими электронами, страница 5

==

==p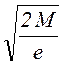

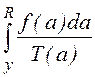
Дифференцируя по  y  и меняя обозначения, получим

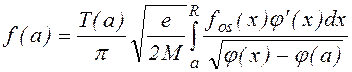.                               (1.1.29)

С помощью  (1.1.15)  и  (1.1.29)  преобразуем уравнение баланса  (1.1.16) к виду

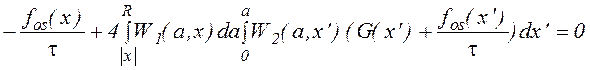. (1.1.30)

При пренебрежении уходом и образованием частиц (для  чего R® ¥, G(x') ® 0 ) решением  (1.1.30)  является Больцмановская функция 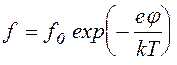, использованная в [86] . Для определения  константы  f₀  необходимо учесть баланс образующихся и уходящих частиц. В [86] поток уходящих частиц принят равным произведению их равновесной концентрации на границе ямы и тепловой скорости и таким образом

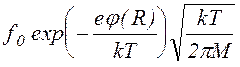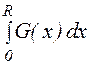=                                (1.1.31)

Tакая оценка для скорости ухода представляется  завышенной,  поскольку, как  правило, концентрация  частиц  вблизи  границы уменьшается по сравнению с равновесной вследствие краевых  эффектов, но даже при таком допущении модель  [86] дает  завышенные значения ионной плотности, что связано  с  неучетом  ухода частиц в продольном направлении, в том  случае, если продольное распределение потенциала монотонно [84], т.е не  содержит  локальных ловушек для ионов.

1.2. Кинетическое уравнение с учетом

продольного движения частиц

При выполнении некоторых  условий, рассматриваемых  ниже, предложенный подход можно использовать и при анализе продольного движения частиц. Пусть j(x,z) = j₀(z)+ j₁(x), где j₀(z) - монотонная функция. Если расстояние  l_T , проходимое частицей вдоль оси  z  за время равное периоду  поперечных  колебаний, отвечает условию  l_T << L, где  L - длина рассматриваемой области в продольном направлении, то от функции  распределения  захваченных  частиц  f_os(z,v_z,x,v_x) можно перейти, как это рассматривалось выше, к функции  f(z,v_z,a). Такой подход в определенном смысле, аналогичен диффузионному приближению  (применяемому при анализе процессов, характерный пространственный масштаб  которых  существенно превышает длину свободного пробега, а  временной  характерное время между столкновениями) и может быть  применен  для анализа процессов ,  характерный продольный масштаб которых  существенно превышает величину  l_T, а временной среднее  значение периода колебаний. Для рассматриваемой задачи, ухода частиц  в продольном  направлении, существенные  изменения  концентрации частиц и продольного электрического поля происходят  обычно на длине l_z ~L  и можно провести следующие оценки для условий  применимости предлагаемого подхода. Пусть j_z  - продольное  изменение потенциала,  T_os - период поперечных колебаний,

T_os ~ R / <v_x> ~ 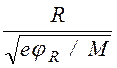     ,                                     (1.2.1)

и, следовательно, должно выполняться

l_T  ~ <v_z>T_os ~ 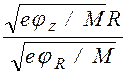<< L .                                    (1.2.2)

Таким образом, глубина потенциальной ямы должна отвечать условию

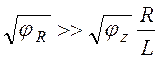                                                              (1.2.3)

Если продольное поле существенно меняется на длине l_z,  меньшей чем  L, то в (1.2.3)  вместо  L  надо подставить  l_z. Кроме того, если продольное электрическое поле мало и характерная скорость частицы   <v> ~ (kT/M)^1/2, то в  (1.2.3) j_z следует заменить на kT/e. Предложенный подход применим при  различных соотношениях между величинами L и l, т.е его можно использовать  не  только при анализе распределения в области в  области  дрейфа  пучка, когда L<<l, но и при выполнении обратного условия L>>l, что часто реализуeтся в газовых разрядах. В этом случае, очевидно, необходим учет влияния столкновений на распределение частиц.  Обязательным является лишь выполнение  условия  низкого  давления (1.1.5)  для поперечного движения. Следует заметить, что при  некоторых условиях учет столкновений будет необходим даже в случае L<<l, т.к при большой глубине потенциальной ямы частица  за счет поперечных колебаний может пройти путь, сравнимый  с длиной свободного прoбега. Оценим  глубину  потенциальной  ямы  в этом случае. Характерное время ухода частицы в  продольном направлении t_z~L/<v>, число  поперечных  колебаний за это время ~t_z/T_os , и если путь