Неупругие столкновения ионов и электронов с атомами

Неупругие столкновения ионов и электронов с атомами

Для неупругих процессов не возникает той проблемы, которая  заключается в расходимости полного сечения и характерна для упругих  процессов. Сечения неупругих процессов всегда являются конечными,  так как для перевода атома в возбужденное и тем более  ионизированное состояние необходимо довольно сильное воздействие на  него с передачей энергии по крайней мере не меньшей чем порог  ионизации или возбуждения. Ясно, что пролетающая на большом  расстоянии от атома частица не может оказать такое сильное  воздействие, что и обуславливает конечность сечения.

1. Порог и сечение реакции ионизации

Основным из газоразрядных процессов, обуславливающим саму  возможность возникновения и горения разряда, является ионизация.  Для того, чтобы удалить электрон из атома, необходимо сообщить ему  энергию по крайней мере не меньшую чем энергия его связи в атоме.  Оценить эту энергию связи для внешнего или валентного электрона можно используя следующее соотношение

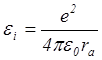
где r_a – радиус атома, совпадающий с радиусом орбиты внешнего электрона. Однако в атомной физике энергию принято измерять не в джоулях, а в электронвольтах. Чтобы перейти к этой единице измерения нужно поделить на заряд электрона. Соответствующую разность потенциалов, которую необходимо пройти частице, чтобы приобрести энергию, равную энергии связи, называют потенциалом ионизации I_i (I_i = e_i /e). Энергия ионизации по порядку величины составляет  ~   10 эв для любых видов атомов.

Наиболее легко ионизуются атомы  щелочных металлов, а среди них самый легкоионизуемый элемент это  цезий - 3.9 эв, а наиболее тяжело атомы инертных или благородных  газов, причем самый высокий потенциал ионизации у Не - 24.6 эв.  Существует довольно много различных механизмов ионизации, но  наиболее важным, по крайней мере в физике газоразрядных процессов  является ионизация электронным ударом. 

А + е ® А⁺ + е + е.

Как и все другие механизмы  ионизация электронным ударом является пороговым процессом и может  произойти лишь в том случае, если энергия налетающего электрона  превышает порог ионизации e > e_i. Таким образом при e < e_i сечение  ионизации равно 0. При  e > e_i с увеличением энергии сечение  сначала возрастает, затем достигает максимума и начинает монотонно  уменьшаться. Такая качественная картинка имеет место для любого  вида атомов, хотя количественные отличия конечно есть, связанные  уже хотя бы с тем, что порог ионизации меняется от атома к атому,  но тем не менее анализ результатов экспериментов показал, что если  зависимость s(e) представить в следующем виде

s(e) = 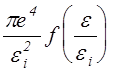, то функция f уже практически не зависит от атомного номера. Все  экспериментальные точки с небольшим разбросом укладываются на одну  кривую. В рамках классической механики в 1912 году Томсоном было  получено следующее простое выражение для f(x):

f(x) = (x-1) / x² где x = e/e_i. При получении этой формулы рассматривалось взаимодействие двух  электронов: налетающего и неподвижного и рассчитывалась вероятность  того что переданная энергия будет больше чем eI_i

 

    V/2             c                   

 

                     v

 

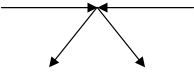
Обозначим скорость налетающего электрона буквой V. Тогда в системе центра масс налетающий и неподвижный электроны летят навстречу друг другу со скоростью V/2 и поворачивают в результате рассеяния на углы c и p-c соответственно. Используя теорему синусов определим скорость v, которую приобретет в Л-системе неподвижный электрон.

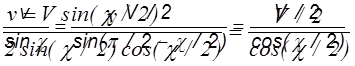Соответственно энергия, переданная налетающей частицей неподвижной частице определяется следующим выражением

Сечение рассеяния в интервал углов dc определяется формулой Резерфорда

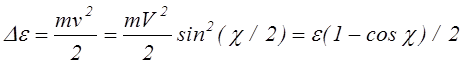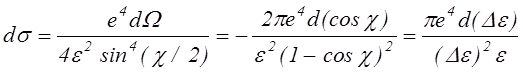Интегрируя по переданной энергии от энергии ионизации до энергии налетающего электрона и учитывая, что на внешней оболочке может находится не один а несколько так называемых валентных электронов, получим полное сечение ионизации

где Z – число валентных электронов. Полученная формула вполне может служить для оценок по порядку  величины, но точного количественного согласия с экспериментом не  дает, так как конечно процесс ионизации как и другие электронные  процессы должен рассматриваться квантовой механикой. Но в рамках  квантовой механики эта задача пока не решена и для проведения  расчетов лучше всего пользоваться непосредственно  экспериментальными данными либо их аппроксимациями.

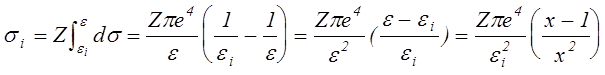Очень удобной и часто используемой является формула Дравина, в которую по сравнению с Томсоновской введен логарифмический множитель. Для сечения передачи энергии получается

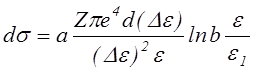Где e1 – энергия возбуждения первого уровня, а и b коэффициенты порядка 1, которые подбираются эмпирически, так чтобы сечения возбуждения и ионизации наилучшим образом совпали с экспериментальными данными. Поскольку в логарифм не входит переданная энергия то интегрирование выполняется аналогично и в формуле для сечения ионизации появляются те же поправки.

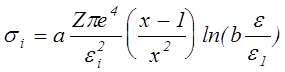Существенным достоинством этой формулы считается то, что она правильно передает ход сечения в пределе больших энергий s~lne/e. Разумеется возможно и использование других приближенных формул. Например в  книге Смирнова "Физика слабоионизованного газа" предложены  следующие аппроксимации