Неупругие столкновения ионов и электронов с атомами, страница 2

f(x) = (x-1) / (x(х+8))

- сверху

f(x)=(x-1)/(x+0.5)(х+10)

- снизу Кроме того в тех случаях, когда энергия электрона незначительно  превышает порог ионизации широко используется простая линейная  аппроксимация

s_i = С (e - e_i ).

2. Частота и константа ионизации

Если рассмотреть некоторый гипотетический электрон обладающий  энергией e, который после ионизации и утраты энергии тут же  восполняет утраченное и вновь приобретает энергию e и  соответственно скорость v=(2e/m)^1/2, то в единицу времени такой  электрон находясь в газе с плотностью N испытает

n_i = Ns_i(e)v(e) ионизирующих столкновений, n_i - частота ионизации. Если имеется не один а некоторый ансамбль электронов с  некоторым распределением по энергии f(e) (òf(e)de=1), то для того чтобы определить частоту ионизаций,  совершаемых в среднем одним электроном, необходимо произвести  усреднение по спектру

n_i = òNs_i(e)v(e)f(e)de = N<s_i(e)v(e)> = Nk_i,

k_i =<s_i(e)v(e)>- константа ионизации, которая представляет собой  частоту ионизации отнормированную на единичную концентрацию k_i = n_i / N,  или более полное название константа скорости реакции ионизации.  В случае Максвелловского распределения

f(e)=2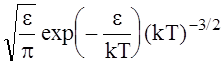

и при использовании линейной аппроксимации s_i = С(e - e_i ) для частоты  ионизации получается следующее выражение

n_i  = N<v>C (e_i +2kT)exp(-e_i/kT)

где     <v>=(8kT/pm)^1/2-  средняя теловая скорость электронов при  максвелловском распределении с температурой Т. Чтобы получить полное число актов ионизации совершаемых ансамблем  электронов в единицу времени в единице объема необходимо умножить частоту ионизации на электронную концентрацию 

(dn_i/dt) = n_in_e = kNn_e.

Скорость ионизации пропорциональна концентрациям реагирующих  частиц, а к-т пропорциональности есть константа этой реакции

3. Возбуждение и ступенчатая ионизация

Процесс возбуждения заключается в переводе одного из  электронов атома из основного состояния в состояние с большей  энергией. е + А ® е + А^*

Энергия связи при этом соответственно уменьшается. Вид сечения возбуждения в целом качественно похож на вид сечения  ионизации. 0 при энергии ниже порога возбуждения, затем резкий рост  и после достижения некоторого максимума спад.

Поскольку  возбужденных уровней много, то следует вообще говоря различать  сечения возбуждения для каждого уровня. Вычислить полное сечение возбуждения можно например воспользовавшись формулой Дравина для сечения передачи энергии

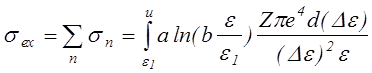где u=e_i при e > e_i , u=e при e < e_i .

Процесс, состоящий из 2-х этапов: возбуждения и последующей  ионизации возбужденного атома

А^* + е ® А⁺ + е + е получил название ступенчатой  ионизации. Если электрон взаимодействует с возбужденным атомом, то  вероятность ионизации существенно выше, чем при взаимодействии с  атомом находящимся в основном состоянии, но проблема в том чтобы  обеспечить достаточно большую концентрацию возбужденных атомов. Они  как известно являются нестабильными и как правило довольно быстро  возвращаются возвращаются в основное состояние с излучением фотона,  не успев повстречаться с электроном и испытать ионизацию.  Исключение составляют так называемые метастабильные атомы, у  которых вероятность такого перехода мала и они могут достаточно  длительное время находится в возбужденном состоянии. Кроме того существует еще одно обстоятельство, способствующее увеличению концентрации возбужденных атомов. Это то, что фотон излученный  атомом и обладающий энергией в точности равной разности энергий  возбужденного и основного уровня является так называемым  резонансным фотоном и может быть с высокой вероятностью поглощен  другим атомом, который в результате перейдет из основного в  возбужденное состояние. Роль этого процесса особенно важна при  высоких давлениях когда фотоны не уходят за пределы газоразрядного  промежутка, а вновь и вновь излучаются и поглощаются. Происходит  своего рода блуждание резонансного излучения по области разряда,  что также способствует увеличению концентрации возбужденных атомов.