Спектр поглощения и излучения в безпримесных кристаллах, страница 2

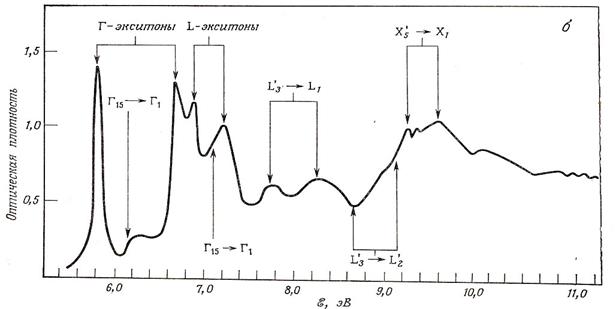
Рис. 2. Спектр поглощения в экситонные состояния KI (узкие полосы), образованных вблизи максимумов и минимумов валентной зоны и зоны проводимости, представленных на следующем рис.3.

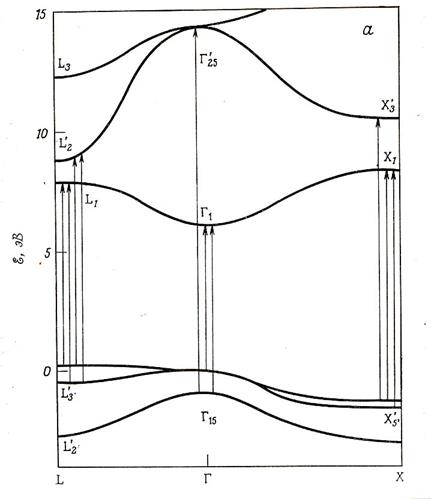
Рис. 3. Зонная структура KI. Вертикальными стрелками указаны экситонные переходы, представленные на предыдущем рис.2.

Причем при поглощении этих полос кристалл остается не способным проводить электрический ток. Появление этих полос, как в поглощении, так и в излучении не объясняется зонной теорией, но оно просто объясняется экситонной теорией. Суть ее заключается в следующем.

В результате поглощения кванта света электрон из валентной зоны переходит в зону проводимости. В ней появляется свободный электрон, а в валентной зоне – свободная дырка с элементарным положительным зарядом и эффективной массой порядка эффективной массы электрона. То есть образуется электронно-дырочная пара. Каждая из этих частиц может двигаться по кристаллу независимо друг от друга. Однако в поле любого положительного заряда, в том числе и в поле дырки, для свободного электрона возникают ряд дискретных, но уже связанных состояний. Такая система называется экситон – возбуждение. Экситон, уже как связанные электрон и дырка, может двигаться по кристаллу – это свободный экситон или оставаться неподвижным – это локализованный экситон. Появление в диэлектрике или полупроводнике экситона не приводит к увеличению электропроводности, так как экситон является электрически нейтральным образованием – квазичастицей.

При движении экситона его импульс определяется волновым вектором , модуль которого может принимать значения в интервале 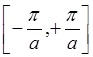, где a – постоянная кристаллической решетки. То есть каждому состоянию экситона соответствует некоторая полоса энергетических уровней, определяемых вектором k, которые располагаются в запрещенной зоне вблизи дна зоны проводимости на характерном удалении от него на десятые доли электроновольта. Оптические переходы возможны только в определенное состояние каждой из этих полос, которое определяется равенством волновых векторов экситона  и фотона . При этом спектры поглощения и излучения имеют линейчатую структуру, заканчивающуюся границей серии, которая в общем случае не совпадает с максимальной длиной волны межзонного перехода. С теоретической точки зрения различают экситоны большого радиуса, которые называются экситонами Ванье-Мотта, и экситоны малого радиуса – экситон Френкеля.

Размеры экситона Ванье-Мотта, т.е. расстояние между электроном и дыркой, велико по сравнению с постоянной кристаллической решетки. В этом случае взаимодействие электрона и дырки можно рассматривать как кулоновское взаимодействие двух точечных зарядов, ослабленное в c раз, c - диэлектрическая проницаемость кристалла. Решение уравнения Шредингера для такой системы дает выражение для собственных значений энергии экситона, очень похожее по виду на выражение для атома водорода

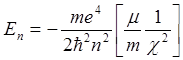,                                        (3)

отличающееся от него членом в квадратных скобках. n – главное квантовое число, 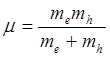 - приведенная масса экситона, m_e и m_h – эффективные массы электрона и дырки в кристалле, m – масса свободного электрона. Радиус экситона Ванье-Мотта определяется также как и для атома водорода, и он равен

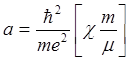.                                                (4)

Откуда видно, что экситоны большого радиуса могут образовываться в кристаллах с большой диэлектрической проницаемостью.

Экситон Френкеля представляют как возбуждение изолированного иона. Это представление называется приближением сильной связи. В этом приближении экситонное возбуждение в простом кубическом кристалле определяется сравнительно узкой энергетической зоной

,                    (5)