Адиабатический потенциал. Конфигурационные кривые. Принцип Франка-Кандона. Электронно-колебательная структура спектра, страница 2

Согласно классическому закону движения осциллятор наибольшее время проводит в поворотных точках, находящихся на конфигурационных кривых, - это точки пересечения колебательных уровней с конфигурационными кривыми. Поэтому в классическом варианте принцип Франка-Кондона полагает, что наиболее вероятными являются переходы между поворотными точками начального и конечного состояний. Т.е. вертикальные стрелки, изображающие переходы на диаграммах, должны начинаться и заканчиваться на конфигурационных кривых. В таком варианте принцип хорошо описывает переходы в молекулах, в которых энергетическое расстояние между колебательными уровнями достаточно велико. Вообще говоря, электронный переход может произойти из любой точки потенциальной кривой, в какой колеблющая система может оказаться при данной температуре. Однако вероятность перехода зависит от вероятности нахождения системы в состоянии с той или иной координатой. При непрерывном колебательном спектре в определенном частотном интервале, который характерен для фононов акустической ветви, эта последняя вероятность описывается кривой Гаусса, максимум которой соответствует минимуму потенциальной (конфигурационной) кривой. Поэтому и распределение энергии в спектре поглощения и излучения в твердых телах (контур полос поглощения и излучения) также часто оказывается гауссовым:

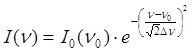,                                           (1)

где n₀ – частота (волновое число), соответствующая максимуму интенсивности I₀(n₀), Dn - ширина полосы.

Из изложенного следует, что принцип Франка-Кондона сочетает в себе элементы классической и квантовой механики. Рассмотренный материал позволяет сделать ряд обобщений, проясняющих явления люминесценции и поглощения света в твердых телах.

1). Колебательные переходы. Переходы между энергетическими уровнями центров люминесценции и поглощения в твердых телах, как правило, не являются чисто электронными, а являются электронно-колебательными. Это приводит к тому, что в спектрах излучения и поглощения кристаллов вместо узких одиночных линий, характерных для свободных атомов и молекул, наблюдаются широкие бесструктурные или слабоструктурированные полосы. Их ширина определяется разностью равновесных расстояний от центрального иона (дефекта) до лигандов в основном R₀ и возбужденном R_ex состояниях – DR=|R₀ – R_ex|. В свою очередь величина DR зависит от орбитальной электронной конфигурации в основном и возбужденном состояниях перехода. Электронные переходы типа:

,                                   (2)

осуществляемые с изменением электронной конфигурации, дают широкие полосы шириной порядка Dn»1000 см^-1. Такие спектральные полосы характерны для разрешенных по спину (DS=0) d«d переходов. Электронные переходы без изменения орбитальной электронной конфигурации дают относительно узкие линии шириной Dn»10-100 см^-1. К таким переходам относятся все f«f переходы и интеркомбинационные (DS¹0) d«d переходы, например, хорошо известные R-линии Cr³⁺ в рубине – переход .

Чисто электронный переход – это переход, при котором колебательное состояние решетки не меняется V=const. Такой переход дает бесфононную или нуль-фононную достаточно узкую линию. Совокупность бесфононных переходов V^*_i«V_i между разными колебательными уровнями i¹const, но при DV=0 (V и V^* - колебательные квантовые числа основного и возбужденного электронного состояний) образуют в спектре чисто электронную не элементарную, а квазилинию, являющуюся суперпозицией целого набора бесфононных линий. Длины волн центров отдельных нуль-фононных линий не совпадают друг с другом из-за неравенства энергии колебательных квантов с разными колебательными квантовыми числами в основном и возбужденном электронном состояниях. Поэтому контур квазилинии шире контура отдельных нуль-фононных линий и хорошо описывается гауссовой кривой типа (1).

Спектр собственных частот нормальных колебаний – фононов идеального кристалла с двухатомной элементарной ячейкой вдоль выделенного кристаллического направления представлен на рис.2 в виде зависимости от модуля волнового вектора k.

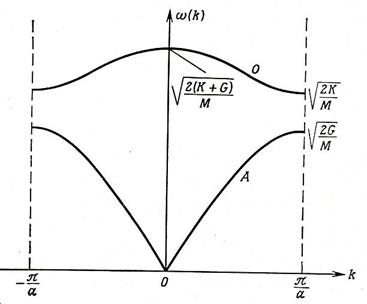
Рис.2. Спектр фононов (закон дисперсии) для двухатомной линейной цепочки. Нижняя ветвь – акустическая, верхняя – оптическая.

Нижняя ветвь разрешенных нормальных колебаний называется акустической, и соответствующие ей фононы называются акустическими. Это название обязано тому, что при малых k закон дисперсии этой ветви имеет форму w=ck, характерную для звуковых волн. Диапазон частот акустических фононов ограничен снизу w=0 при k=0, а сверху – частотой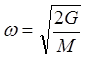 при k=p/a, где G – константа упругости между атомами одинакового заряда массой M, расположенных в разных, но ближайших элементарных ячейках, a – постоянная решетки. В моноатомных кристаллах, например, в металлах, имеется только акустическая ветвь.