Лекция 3
Расчет асимптотических значений энергии частиц при упругом столкновении
1. С точки зрения радиационной физики твердого тела, первичный процесс (мы об этом говорили) – это взаимодействие между излучением и твердым телом, приводящее к выбиванию атома из его места в решетке. Это происходит, если энергия отдачи (энергия атома отдачи) > энергии его связи в решетке.
Обозначим:
M1,
![]() , E1
– параметры налетающей частицы до столкновения;
, E1
– параметры налетающей частицы до столкновения;
θ1 – угол рассеяния;
![]() – ее
конечная скорость.
– ее
конечная скорость.
М2, ![]() , Е2(=0) – параметры
частицы-мишени до столкновения;
, Е2(=0) – параметры
частицы-мишени до столкновения;
![]() –
конечная скорость второй частицы;
–
конечная скорость второй частицы;
θ 2 – угол отдачи.
2. Это изначальный первичный процесс для ФТТ, но он состоит как бы из двух процессов:
1 – столкновения заряженной частицы с ядром (мы рассматриваем тяжелые заряженные частицы),
2 – преодоление атомом отдачи энергии связи.
3. Процесс столкновения мы будем называть простейшим первичным процессом.
Уравнения в системе, связанной с центром масс столкновения частиц
![]() G М1,
G М1, ![]()
![]()
![]()
![]()
![]() M1,
M1, ![]() (М1+М2),
(М1+М2),
![]() М2,
М2, ![]() =
= ![]()
М2,
![]()
Такую систему называют с-системой
![]() L – lab сист.
L – lab сист.
![]()
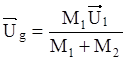
Вычитая ![]() из
всех скоростей, переходим к с-системе.
из
всех скоростей, переходим к с-системе.
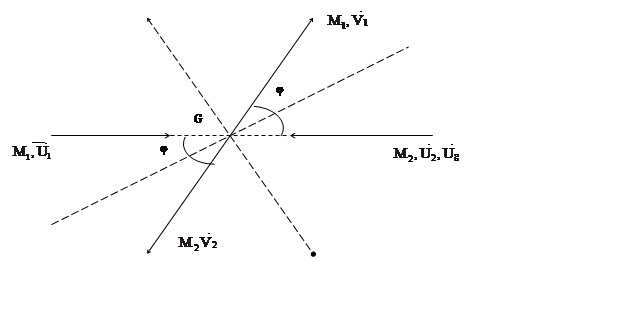
Обозначения в с-системе:
![]()
![]() – до соударения
– до соударения
![]()
![]() – после соударения
– после соударения
 |
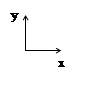
![]()
М1 до столкновения М1 после столкновения
![]()
![]()
![]() =
=![]() +(–
+(–![]() )
)
![]() –
–![]()
![]() =
= ![]() +(–
+(–![]() )
)
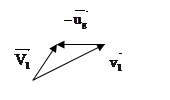
М2 до столкновения М2 после столкновения
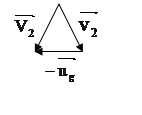
![]()
–![]()
![]() =
=![]() +(–
+(–![]() )
)
![]() =
= ![]() +(–
+(–![]() )
)
Поскольку G
считается в покое, ![]() и
и ![]() противоположно направлены.
противоположно направлены.
Закон сохранения энергии и импульса имеет следующий вид:
![]() (1)
(1)
![]() (2)
(2)
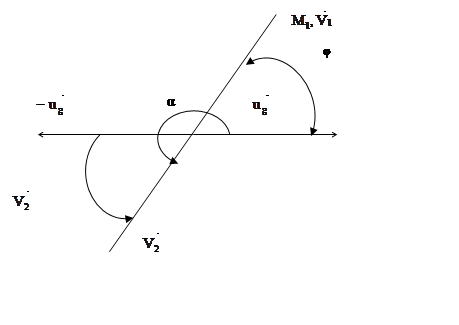
Проецируя (2) на оси х и у, получаем
х: M1U1 – M2Ug = (M1V1 – M2V2) cos φ (3)
y: M1V1 – M2V2 = 0 Þ M1V1 = M2V2 (4)
С учетом этого соотношения из (4) следует, что
M1U1 = M2Ug (5)
|
Тогда (6)
Проецируем на биссектрису угла:
![]()
![]()
![]()
![]()
|
||||
|
||||
Þ
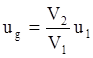
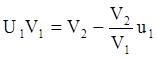
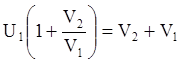
|
|
||||
Þ
Далее:
|
|
![]()
 |
![]()
![]()
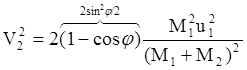
![]()
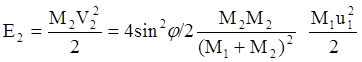
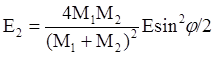
![]()
где Е2 – это энергия отдачи (энергия атома отдачи). Получение соотношения аналогично соотношению для комптоновского рассеяния (упругое рассеяние γ-квантов на электронах).
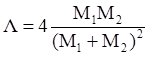 –
коэффициент передачи энергии.
–
коэффициент передачи энергии.
При φ = π (лобовое соударение) происходит максимальная передача энергии:
![]()
(в с-системе частицы при этом сближаются и удаляются по одной прямой).
Когда φ = 0, рассеяния нет, и Е2 = 0. В реальном случае, когда заряд частицы взаимодействует на расстоянии посредством электрического поля, этот случай соответствует большему значению прицельного параметра.
 |
В задачах с радиационными нарушениями вводят E2 – минимальная энергия, необходимая для создания радиационного повреждения.
![]()
где ![]() – минимальная энергия,
необходимая для создания радиационного повреждения (для которой
– минимальная энергия,
необходимая для создания радиационного повреждения (для которой ![]() – максимальная энергия отдачи).
– максимальная энергия отдачи).
Нас будут интересовать соответственно только
процессы, в которых ![]() .
.
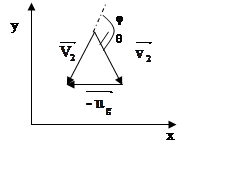 Связь между Θ2 и φ
можно получить, проецируя соотношение
Связь между Θ2 и φ
можно получить, проецируя соотношение ![]() на оси
х и у.
на оси
х и у.
![]()
![]() y: V2sinφ = V2sinθ2
y: V2sinφ = V2sinθ2
V2cosφ + V2cos θ2 = ug
Поскольку ug = V2, имеем
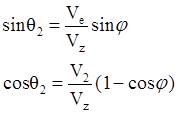
|
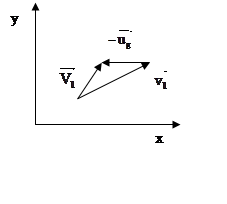
Аналогично,
проецируя соотношение ![]()
![]() на оси
х и у, можно получить соотношение для θ1:
на оси
х и у, можно получить соотношение для θ1:
 |
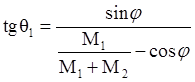
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.