Классификация ионов. Быстрые легкие ионы, обычные кулоновские столкновения

Лекция 7

1. Классификация ионов

Взаимодействие ионов разной массы и энергии с веществом описывается внешне различными закономерностями (несмотря на то, что их поведение описывается одними и теми же общими законами, заложенными, в частности, в уравнении (5.13)).

Различают следующие наиболее характерные случаи:

1)  Быстрые легкие ионы  с энергией Е > 10⁶ эВ.

2)  Осколки деления (тяжелые ионы с Е₁ ~ 10⁸ эВ и М₁ ~ 10² а.е.м.), испускаемые в результате деления тяжелых ядер

3)  Тяжелые ионы с Е₁ < 10⁶ эВ: сюда относятся имплантируемые в вещество тяжелые ионы и атомы отдачи.

Точное решение задачи о столкновениях при заданных p и V(r) позволяет определить ρ₀ (см. формулу (5.16)).

Минимальное расстояние ρ₀, до которого сближаются сталкивающиеся частицы, имеющие различную массу и энергию, в зависимости от Е₂ приведены на рис. 6.1.

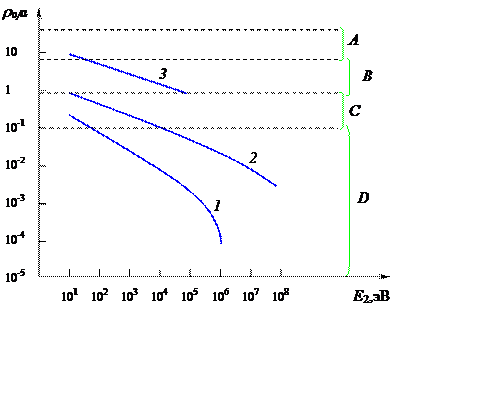
Расстояние максимального сближения r₀ как функция E₂:

;

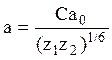1 – протоны 20 МэВ в Cu (быстрые легкие ионы) (М = 1);

2 – Хе⁺ 70 МэВ в Cu (осколки деления) (М = 131);

3 – Cu Е = 50 кэВ в Сu (тяжелые ионы, атомы отдачи) (М = 64);

A - потенциал Б-М; B - потенциал r^{-2, C} – экранированный кулоновский (Т-Ф) потенциал, D - кулоновский потенциал

Рис. 7.1.

В соответствии с этим результатом, для разных категорий ионов необходимо использовать различные приближения для потенциала, в точном соотношении (5.13) или в приближенных теориях.

1.1.  Быстрые легкие ионы, обычные кулоновские столкновения

Эти столкновения изучал Резерфорд. Он изучал прохождение α-частиц через металлы. Резерфорд заметил, что частицы отклоняются достаточно редко на большие углы. Это привело его к предположению, что отрицательный заряд атомов сосредоточен в электронных оболочках, а основная масса атома и его положительный заряд сосредоточены в ядре, имеющем очень малые размеры.

Известно, что решение уравнения траекторий для кулоновского потенциала 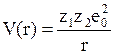  приводит к формуле Резерфорда

                                                  (6.1  )

Более точно уравнение Резерфорда в с-системе записывается следующим образом:

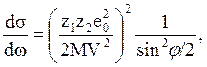                                         (6.2 )

где 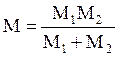      – приведенная масса; V = u₁ – скорость сближения частиц; φ – угол рассеяния.

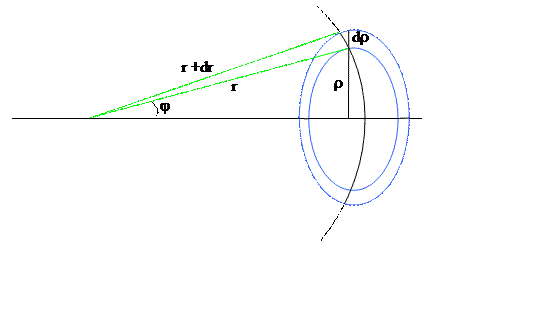
Поскольку dω – телесный угол, то 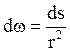 (ds = 2πρdρ, ρ = r sinφ, dρ = rdφ) и

|dω = 2π sinφ dφ|                                           (7.3)

пли                             dω = 4π sinφ/2 cosφ/2 dφ.                            (7.4)

Тогда 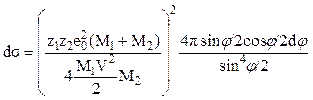                                             .               (7.5)

Введем                                        откуда

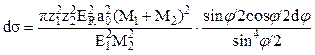 ,                  (7.6 )

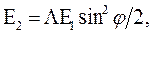
учитывая, что

,

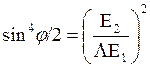, получаем 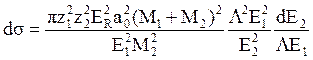                              ,                   (7.7)

где 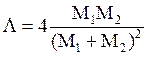                                                      –коэффициент предачи энергии.

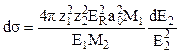                                   (7.8)

                                                                               

 

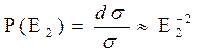
Для приближения твердых сфер мы получили, что 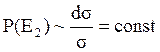  , а именно        .

                     

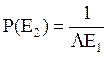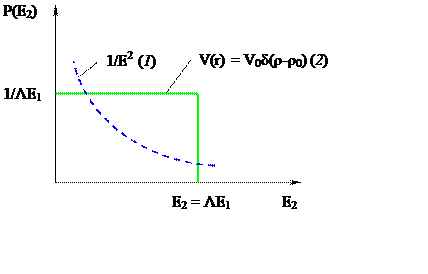
Плотности вероятности образования атомов отдачи для кулоновского потенциала (1)

и короткодействующего потенциала (приближения твердых сфер) (2)

Рис. 7.2.

Оказывается, Р(Е₂) зависит от вида потенциала.

Полное сечение                                σ_р = ∫dσ.                                                         (7.9)

В пределах от 0 до ΛЕ₁ этот интеграл расходится, таково свойство степенных интегралов. Поэтому мы будем интегрировать от ₂ (тем более, что нас интересуют только такие энергии).

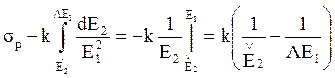                           (7.10)

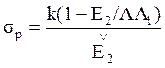                                      (7.11)

Тогда для 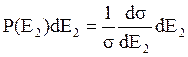 имеем

 

(7.12))

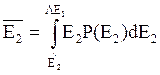                                                   (7.13)

 

(7.14)

Обычно знаменатель близок к единице, и изменение  при изменении Е₁ идет очень медленно, и, как правило,  лишь в несколько раз превышает Е₂. То есть наиболее велика вероятность образования ионов отдачи с малой энергией.

Можно показать, что для легких ионов классическое приближение, в котором мы получили результат, справедливо для относительно малых энергий – от нескольких кэВ до нескольких сотен кэВ. Для тяжелых ионов и тяжелых мишеней это справедливо только для высоких энергий(10⁴–10⁷ кэВ).