Программа статистического наблюдения компаний рынка парфюмерии и косметики в РФ, страница 13

Источник: Сайт Банка России

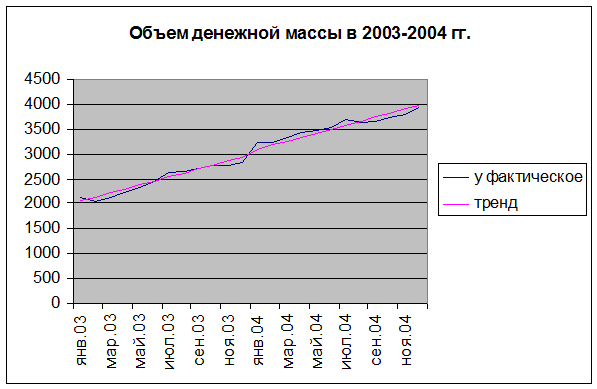
Построим график динамического ряда. Из графика видно, что денежная масса имеет явную тенденцию к увеличению, причем линия тренда, которая здесь подходит – прямая . Параметры уравнения прямой можно определить методом наименьших квадратов, при этом следует временные периоды обзначить так, чтобы их сумма равнялась нулю. Система уравнений будет иметь вид:

Из этой системы получаем прямую

Для проверки ряда динамики на наличие сезонной компоненты следует вычислить индексы сезонности.

Таблица 11.2. Индексы сезонности

Как видно, из таблицы значения индексов сезонности очень высоки, близки к единице. 

Построим график абсолютных и относительных отклонений выровненных  значений от фактических и проверим их на автокорреляцию. Для этого вычислим коэффициент корреляции между соседними значениями отклонений.   Коэффициент автокорреляции по абсолютным отклонениям  равен 0,97, по относительным – 0,41. Из графика видно, что амплитуда отклонений равномерна на протяжении всего периода времени кроме лета 2004 года.

Для того, чтобы построить гармоническую модель за 2003 год, применим ряд Фурье

Используя статистические таблицы, найдем параметры для четырех гармоник, при k=1, 2,3,4.

Теперь найдем расчетные значения у для каждой гармоники.

Таблица 11.3.