Экономика и менеджмент \ Статистика

Программа статистического наблюдения компаний рынка парфюмерии и косметики в РФ, страница 10

Таблица 7.2.

№ ПП

Наименование

Собств. капитал, т.р.

1

Сбербанк РФ

97814270

2

Внешторгбанк

49401661

3

Международный московский банк

3458568

4

Райфазенбанк

1797350

5

Промсвязьбанк

1924826

6

Газпромбанк

22628282

7

Менатеп Спб

2358453

8

БИН-банк

3307385

9

Номос-банк

4068505

10

Петрокоммерц

5355098

Таблица 7.3.

Пок-ль

Выб. среднее

Предельная ошибка,

Генеральн. среднее

Доверительные интервалы для генеральной средней,

Значение

19211440

9181953

10363171

(1181218; 19545125)

Как видно из таблицы, выборочное среднее попадает в доверительный интервал для генерального среднего.

Задание 8

Построим корреляционную таблицу, характеризующую зависимость прибыли коммерческих банков от объема вложений в гос. ценные бумаги. При этом факторный признак – вложения в ценные бумаги расположим по возрастанию.

Таблица 8.1.

№ ПП

Наименование

Вложения в ценные бумаги, т.р.

Балансовая прибыль, т.р.

1

Возрождение

215

-2085

2

Собинбанк

319

4075

3

МДМ-банк

556

13594

4

Гута-банк

769

17530

5

Автобанк

1157

32306

6

Номос-банк

1873

34061

7

Национальный резервный банк

2762

39690

8

Глобэкс

4367

41824

9

БИН-банк

10345

52143

10

Сургутнефтегазбанк

11657

64123

11

НИКойл

12536

66166

12

ИНГ-банк

11647

72486

13

Промсвязьбанк

16378

80337

14

Еврофинанс

25367

81336

15

«Уралсиб»

43657

113648

16

Райфайзенбанк

44265

121374

17

Банк Москвы

43562

121976

18

Альфа-банк

56742

123689

19

Международный промышленный банк

57468

126351

20

Банк «Зенит»

62534

143335

21

«Менатеп Спб»

65345

154685

22

Петрокоммерц

65243

225519

23

Промышленно-строительный банк

68735

228765

24

Междунардный московский банк

70187

231407

25

Росбанк

3647

251834

26

Газпромбанк

73998

275874

27

Доверительный и инвестиционный банк

78345

553601

28

Ситибанк

86234

755551

29

Внешторгбанк

152435

1308878

30

Сбербанк РФ

3457723

5466392

По рисунку видно, что зависимость результативного признака от факторного имеет место. Причем эта зависимость выражается гиперболой следующего вида: 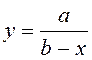. Применив метод наименьших квадратов, находим параметры a и b и получаем следующее уравнение регрессии:

Скачать файл