Циклические коды. Преобразователь кода c дополнением до 2 в код Айкена, страница 3

Номер комбинации	Код с дополнением до 2				Код Айкена
	A	B	C	d	A	B	C	D
12	0	1	0	0	x	x	x	x
13	0	0	1	1	x	x	x	x
14	0	0	1	0	x	x	x	x
15	0	0	0	1	x	x	x	x

Для синтеза преобразования кода нанесем на карты Карно выражения для  A, B, C, D, полученные из таблице 1 (рисунок 5), и проведем считывание минимальным образом.

ab\ cd	00	10	11	01	00	10	11	01	00	10	11	01	00	10	11	01
00	0	1	0	Х	0	1	1	Х	0	1	0	Х	0	0	0	Х
10	Х	1	0	X	Х	1	0	X	Х	0	1	X	Х	0	0	X
11	Х	1	0	1	Х	0	0	1	Х	1	0	1	Х	1	1	1
01	Х	1	0	X	Х	1	0	X	Х	0	1	X	Х	1	1	X
	A				B				C				D

Рисунок 5 – Карты Карно для минимизации исходных функций

Выражения для A, B, C, D, E преобразователя бинарного кода:

A = ab + ab

B = ab + acd + bcd + bcd

C = ab + bcd + bcd + bcd + abcd

D = d

Схема преобразователя кода в программе Proteus показана на рисунке 6.

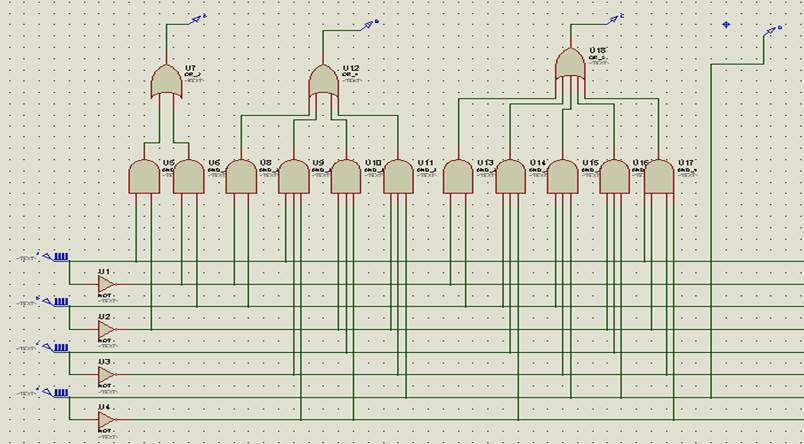
Рисунок 6

Логическая диаграмма в программе Proteus показана на рисунке 7.

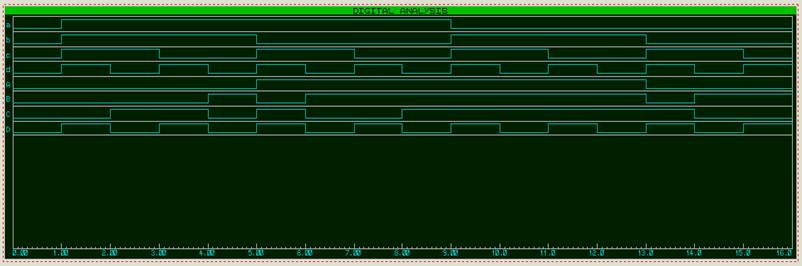
Рисунок 7

2 Проектирование счетчика

Счетчиком называется последовательное устройство, способное подсчитывать количество импульсов, поступивших на его вход. Используется для подсчета числа импульсов, для деления частоты, для формирования или запоминания двоичного кода, соответствующего числу поступивших импульсов.

Основными параметрами счетчиков являются их информационная емкость и быстродействие.

Емкость счетчика определяется максимальным числом сигналов, которое может быть сосчитано, и численно равна коэффициенту пересчета К_сч. После поступления К_сч входных импульсов счетчик возвращается в исходное состояние. Быстродействие счетчика определяется двумя величинами: разрешающей способностью и временем установки очередного состояния.

По направлению счета различают счетчики суммирующие, вычитающие и реверсирующие.

По способу межразрядного переноса различают счетчики с последовательным, параллельным либо комбинированным (последовательно-параллельным) переносом.

Счетчики с последовательными переносом называют асинхронными, с параллельным – синхронными.

Счетчики с произвольным коэффициентом счета – это такие счетчики, которые  имеют К_сч < 2^m, где m – число триггеров. Принцип их построения состоит в исключении некоторых избыточных устойчивых состояний обычного двоичного счетчика путем введения обратных связей.

В качестве примера рассмотрим синтез вычитающего синхронного счетчика с К_сч = 11. Такой счетчик реализуется на основе двоичного четырехразрядного счетчика, в котором исключено, пять устойчивых состояний.

На рисунке 8 отмечены 5 устойчивых состояний – 2, 5, 8, 11, 14.

Рисунок 8

Составляем таблицу состояний счетчика с К_сч = 11(таблица 3).

Таблица 3