Циклические коды. Преобразователь кода c дополнением до 2 в код Айкена, страница 2

Для синтеза преобразования кода нанесем на карты Карно выражения для  A, B, C, D, полученные из таблице 1 (рисунок 2), и проведем считывание минимальным образом.

ab/cd	00	10	11	01	00	10	11	01	00	10	11	01	00	10	11	01
00	0	1	1	0	0	0	0	1	1	1	0	1	1	0	1	0
10	1	0	0	1	1	0	1	1	1	0	0	0	1	0	1	0
11	0	1	0	1	1	0	0	1	1	0	0	1	1	0	1	0
01	1	0	1	0	0	0	1	1	1	1	0	0	1	0	1	0
	A				B				C				D

Рисунок 2 – Карты Карно для минимизации исходных функций

Выражения для A, B, C, D преобразователя бинарного кода:

А = acd + abc + abc + acd + abcd +abcd

B = abc + bcd + bcd + ab

C = ab + bdc + acd + bcd + acd

D = ab + ab

Схема преобразователя кода в программе Proteus показана на рисунке 3.

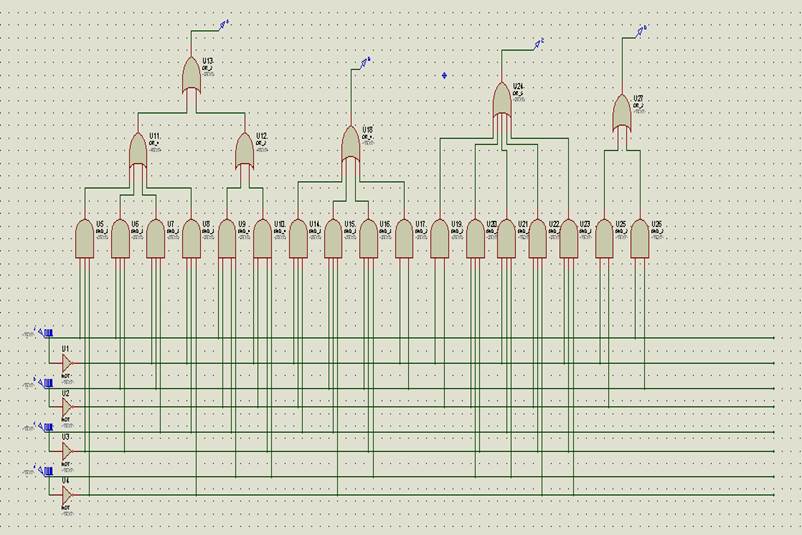
Рисунок 3

Логическая диаграмма в программе Proteus показана на рисунке 4.

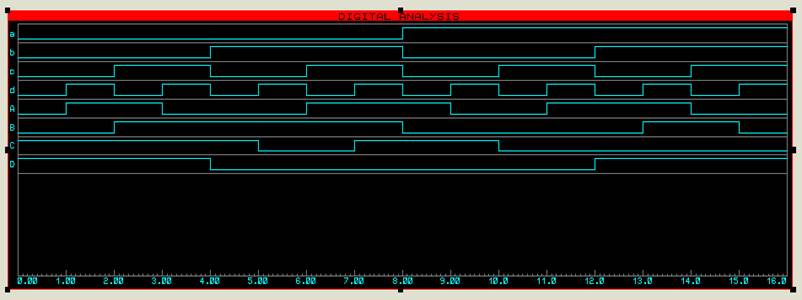
Рисунок 4

1.2 Преобразователь кода с дополнением до двух в код Айкена.

Код с дополнением до 2 характерен тем, что суммирование преобразованного и исходного чисел дает нули во всех разрядах с переносом единицы из старшего бита результирующего числа.

Код Айкена очень похож на прямой двоичный код. Он отличается лишь весом старшего бита (вес старшего бита равен не 8, а 2). Это отличие делает его удобным при определении, находится ли число в верхней половине диапазона от 0 до 9 либо в нижней (достаточно проверить состояние старшего бита).

Строим таблицу истинности аналогичную таблице 1.

Таблица 2 – Таблица истинности для преобразования кода Айкена и кода Джонсона

Номер комбинации	Код с дополнением до 2				Код Айкена
	a	b	c	d	A	B	C	D
0	0	0	0	0	0	0	0	0
1	1	1	1	1	0	0	0	1
2	1	1	1	0	0	0	1	0
3	1	1	0	1	0	0	1	1
4	1	1	0	0	0	1	0	0
5	1	0	1	1	1	0	1	1
6	1	0	1	0	1	1	0	0
7	1	0	0	1	1	1	0	1
8	1	0	0	0	1	1	1	0
9	0	1	1	1	1	1	1	1
10	0	1	1	0	x	x	x	x
11	0	1	0	1	x	x	x	x

Продолжение таблицы 2