Аппараты искусственного кровообращения. Особенности и функции системы кровообращения. Моделирование системы гемодинамики, страница 3

Так как dV/dt = (dP/dt)k, a Q = P/R, то получаем следующее дифференциальное уравнение для описания модели упругого резервуара:

dP/dt = kW(t) – αP(t),                                                                  (7.4)

где a = k/R некоторая обобщенная характеристика сосуда, смысл которой станет ясен из дальнейшего анализа.

Функции W(t) имеет положительное значение только во время систолы, и равно нулю во время диастолы. Точный ее вид неизвестен. Однако, ее можно аппроксимировать ее положительной частью синусоиды. Такое предположение верно, учитывая, что левый желудочек представляет собой пульсирующий насос. Тогда функция W(t) имеет вид:

W(t) = W0sin(tπ/T_c),                             при 0←t←T_c                              

(7.5)

W(t) = 0                                    при T_c←t←T₀                                       где Т_с – время систолы, Т₀ – длительность сердечного цикла.

Обозначим через Р_с переменное давление в период систолы, а через P_д – в период диастолы. Тогда один цикл сердечного сокращения можно рассматривать в виде двух интервалов,изменения давления в течение которых:

dP_с /dt = Csinγ t – αP_с               при 0 ←t ← T_с,                                  

(7.6)

dP_д /dt = - αP_с                           при T_с ←t ← T₀                                   где C = kW,  γ=π/Т_с;  Т₀ = Т_с + Т_д.

Решение этих уравнений имеет вид:

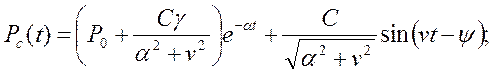                  (7.8)

Р_д(t)=Р₁е^-α(t-Тс)                                                                              (7.9)

Для определения постоянных интегрирования учтем, что давление в начале систолы равно Р₁ = Р_де^-αТс.

Давление в конце систолы и начале диастолы:

Р₀ = (Р₁+В)е^-αТс + Dsin(π - Y).                                                    (7.10)

Здесь В = Сv²/(α² + v²), D= C/ Нетрудно определить, что:

;                                           (7.11)

.                                      (7.12)

Определим порядок величин в выражениях (7.8) и (7.9). Время систолы Т_С обычно составляет десятые доли секунды, примем Т_с = 0,3с, a T₀ = 1с, тогда v = 10. Значение α может быть определено методом катетеризации сердца. Этот метод позволяет установить, что α < 1, следовательно, α² << v² и B = D = kW₀T_c/π, Ψ = arctg10, т.е. Ψ < π/2; max[sin(π - Ψ)] = 1. Определим остальные величины:  е^-αТс = 0,7; е^-αТд = 0,5; е^-αТ0 = 0,37,тогда Р₀ = 1,4 В. Таким образом, при принятых численных значения соотношения (7.8), (7.9) принимают вид:

                                                    (7.13)

                                                                     (7.14)

Воспользовавшись этими уравнениями, можно графически отобразить закономерности изменения давления в аорте за одно сердечное сокращение. Из рис 7.2 видно, что давление во время систолы резко возрастает от значения Р₀ до Р_В, а во время диастолы падает по экспоненциальному закону до значения Р_Н = Р₀.

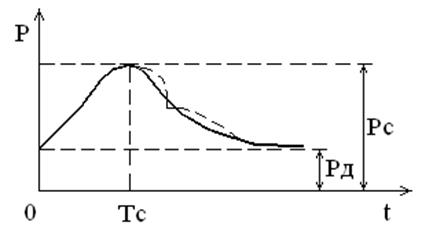
Рис. 7.2 – Теоретическая кривая волны давления в аорте за время одного сердечного цикла.

Экспериментально было показано, что вид зависимости Р_Д(t) отличается от экспоненциальной (на рис 7.2 эта зависимость проведена пунктирной линией). Однако можно аппроксимировать реальную функцию Р_Д(t) экспонентой и определить, таким образом, параметр α а, следовательно, и параметр к. Ошибка такого подхода к определению α и к составит 10–25%.

Модель упругого однокамерного резервуара является, конечно, очень упрощенной моделью системы кровообращения. Однако, полученные выражения позволяют определить связь между медико-биологическими параметрами в главной магистрали системы – аорты. С другой стороны, при создании технических средств обеспечивающих кровообращение, необходимо обеспечить получение аналога пульсовой волны максимально приближенной к естественной волне давления в артериальной системе

Дальнейшее развитие этой теории позволяет получить модели кровообращения в виде двухкамерного и даже многокамерного упругого резервуаров. Это дает возможность получить необходимые требования к системам искусственного кровообращения.

7.3. Аппараты вспомогательного и полного кровообращения