Экспериментальное определение динамических свойств объекта регулирования (Лабораторная работа № 2), страница 2

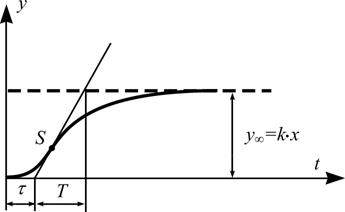
Рис.4. Переходная  характеристика    двухемкостного объекта.

Отрезок времени от начала нанесения возмущения до точки пересечения касательной с осью времени составит запаздывание t.

Отрезок времени от момента пересечения касательной с осью времени до момента пересечения ее с  линией  нового  установившегося  значения выходной величины принимается за постоянную времени объекта Т.

Индивидуальные свойства     различных     объектов,      например одноемкостных,  проявляются  в  том,  что  при  одинаковом  возмущении окажутся различными значения  коэффициента  передачи  К  и  постоянной времени  Т.  Именно  для  их нахождения ставится эксперимент по снятию переходной характеристики. Эти величины определяют характер протекания переходных  процессов,  их динамику и относятся поэтому к динамическим характеристикам объекта.

Следует отметить,    что    для    многих   объектов   переходные характеристики,  полученные при увеличении входной величины и  при  ее уменьшении,   существенно   различны.   Естественно, что  получаются  и различные значения динамических параметров объекта.

4. Численный метод расчета

Кроме графического метода можно воспользоваться численным. Для этого определяют абсциссы точек, ординаты которых равны:  

Y(t^II) = 0,33 у (∞)+Y(0);

Y(t^I) = 0,7 у(∞)+Y(0),

Где у(∞)=У_к –У(0)-приращение кривой разгона за время переходного процесса;

У_к , У(0) – конечное и начальное соответственно значения кривой разгона.

По вычисленным значениям ординат, производя обратное преобразование, находим значения абцисс t^II, t^I , по которым и определяются искомые асимптотические параметры:

τ_з = 0,5 (3t^II- t^I);       Т = 1,25 (t^I - t^II).                                         

Таким образом, при проектировании АСР динамику объекта можно описывать двояко либо точной передаточной функцией (3) ,

W(p)=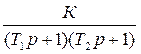,                                                    (3)

либо приближённой (4).

W_э(p)=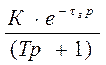                                                (4)

В первом случае используют достаточно точные методы анализа и синтеза АСР (частотные, корневые и т.д.). Во втором – приближённые (графоаналитические). Рассмотрим порядок нахождения Т аналитическим способом.

5. Аналитический метод.

Для проверки точности идентификации в СИАМ набираем схему, изображенную на рис.8.4.

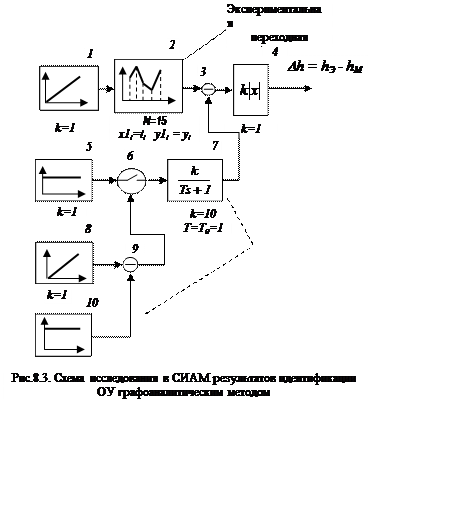Здесь блоки 1,2 моделируют экспериментальную переходную функцию, блоки 5-10 – апериодическое звено с запаздыванием. Выходной сигнал блока 6

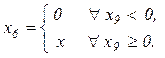
Но сигнал  x₉³ 0тогда, когда разность x₈ – x₁₀³ 0или 

t³k₁₀  (k₁₀ =t., т.е.величина коэффициента k₁₀равна времени запаздывания  t). Таким образом,

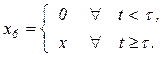
Реальный процесс может продолжаться десятки минут, поэтому  с  целью  сокращения  времени  расчетов  на  ЭВМ необходимо   использовать  масштабирование   во  времени:  t_М = k_Мt.  Если положить k_М = 1/60, то 1 с машинного времени будет соответствовать 1 мин реального процесса. Как при этом изменится передаточная функция (8.3)? Как известно, переменной преобразования Лапласа p соответствует оператор d/dt. С учетом масштабирования ,  dt = dt_М / k_М

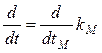 и , тогда формула (8.3) в машинных переменных запишется так:

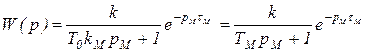.      (8.7)

Таким образом, в схеме СИАМ на рис.8.3 в блоке 2  можно задавать экспериментальную переходную функцию в секундах, в блоке 7 параметр  T₁₁ = T_М  = T₀ k_М = T₀ / 60, в блоке 10 параметр  k₁₁ = t_М =  k_Мt  = t  / 60.