Дискриминантный и кластерный анализ в системе Statistica, страница 5

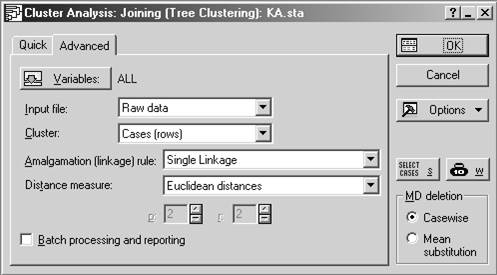
1. выбрать переменные для анализа (Variables);

2. определить вид входных данных (Input): можно вводить таблицу с координатами объектов (Raw data), либо сразу матрицу расстояний между объектами (Distance matrix);

3. определить объекты кластеризации (Cluster): это могут быть переменные (столбцы) (Variables (columns)), либо наблюдения (строки) – Cases (rows). В последнем случае каждая строка таблицы исходных данных есть объект;

4. выбрать метрику, определяющую расстояние между кластерами – Amalgamation (linkage) rile;

5. выбрать метрику, определяющую расстояние между объектами – Distance measure.

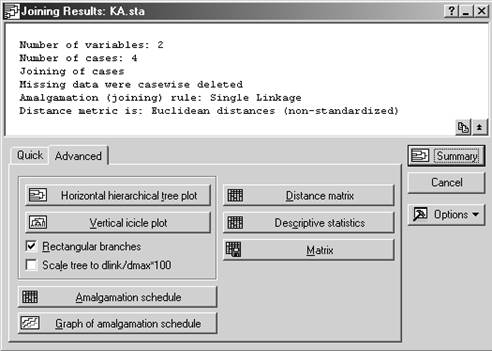
Результаты кластеризации имеют следующий вид:

1)  строится горизонтальная или вертикальная дендрограмма – график, на котором определены расстояния между объектами и кластерами при их последовательном объединении. Древовидная структура графика позволяет определить кластеры в зависимости от выбранного порога - заданного расстояния между кластерами;

2)  выводится матрица расстояний между исходными объектами (Distance matrix);

3)  выводятся средние и среднеквадратичные отклонения для каждого исходного объекта (Discriptive statistics).

Для нашего примера.

Шаг 1. Для метода одиночной связи (Single Linkage).

Шаг 2.

Шаг 3.

     ИЛИ

Шаг 4. Или то же, но в таблице.

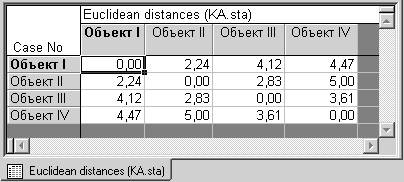
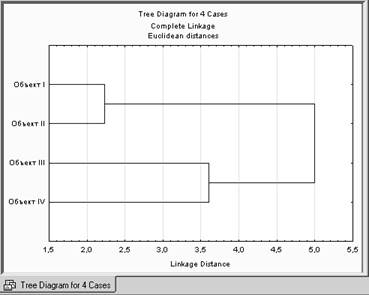Шаг 5. Аналогично, для метода полной связи.

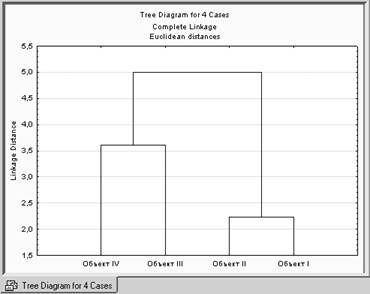      ИЛИ

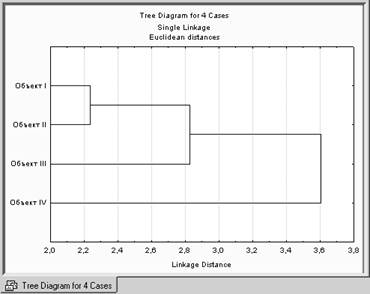
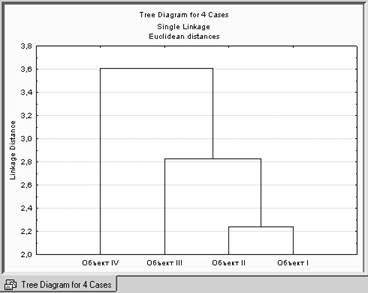
Отрезки дендрограммы проводятся на уровнях, соответствующих пороговым значениям расстояний, выбираемым для данного шага кластеризации.

Например, кластеризация методом одиночной связи (ближайшего соседа) приводит к образованию одного кластера (пороговое расстояние равно 3.6), а кластеризация методом полной связи (дальнего соседа) при таком же пороговом расстоянии равным 3.6, приводит к образованию двух кластеров и т.д.

2.2. Метод К-средних (K-means clustering) относится к группе так называемых эталонных методов кластерного анализа. Число кластеров К задается пользователем. Процедура состоит в следующем. На первом шаге определяют К кластеров – эталонов (это могут быть, например, первые К объектов). Далее каждый объект присоединяется к ближайшему эталону. В качестве критерия используется минимальное расстояние внутри кластера относительно среднего. Как только объект включается в кластер, среднее пересчитывается. После пересчета эталона объекты снова распределяются по ближайшим кластерам и т.д. Процедура заканчивается при стабилизации процесса, т.е. при стабилизации центров тяжести.

Пример 3. Провести методом К-средних классификацию 10 объектов, каждый из которых характеризуется тремя признаками: X, Y, Z.

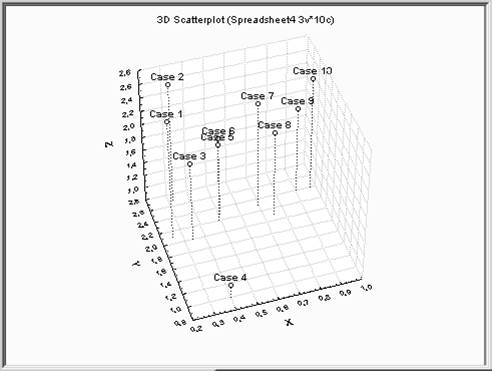
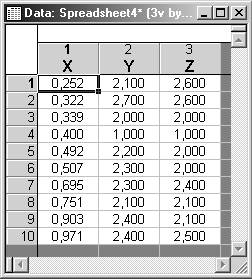
визуализация

данных

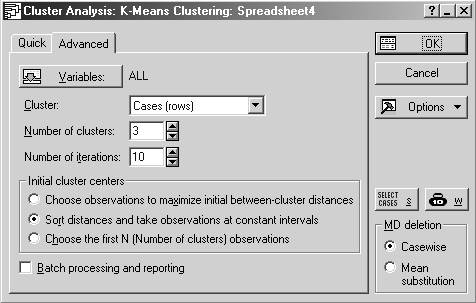
Шаг 1. Запустите модуль Кластерный анализ (Cluster Analysis). Выберите K-means clustering. В появившемся окне выполните следующие настройки:

а) выберите переменные для анализа (Variables): X, Y, Z;

б) определить объекты кластеризации (Cluster): наблюдения (строки) – Cases (rows);

в) задайте число кластеров, равное трем;

г) задайте число итераций;

д) выберите один из трех методов для начального определения центров кластеров (эталонов):

либо выбираются первые N объектов, либо выбираются объекты наиболее максимально отстоящие друг от друга, либо отстоящие друг от друга на одинаковом расстоянии.

Нажмите ОК.

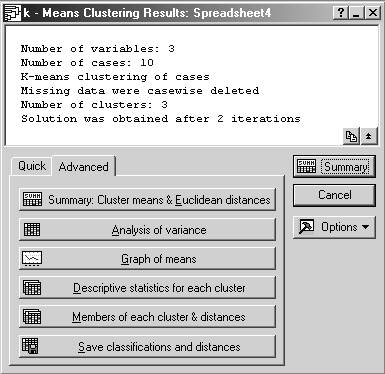
Шаг 2. Результаты кластеризации:

количество переменных: 3

количество строк: 10

метод К-средних для строк

удаление пустых строк из обработки

число кластеров: 3

процедура стабилизировалась после 2 итераций

матрица Евклидовых расстояний;

результаты дисперсионного анализа по каждому признаку;

график распределения центров кластеров;

описательные статистики для каждого кластера;

номера объектов, входящих в каждый кластер,

и расстояния до центра каждого кластера;

Шаг 3. В данном примере объекты распределились следующим образом: