|
№ |
Группа сельхозпредприятий |
Показатель (год) |
||||
|
1996 |
1997 |
1998 |
1999 |
2000 |
||
|
1 2 3 4 5 |
Высокий уровень |
32,5 26,7 22,8 25,8 24,5 |
20,4 22,3 22,1 25,6 22,8 |
28,6 29,8 23,4 26,8 28,5 |
25,3 27,4 25,9 30,7 30,4 |
30,1 29,1 32,7 29,7 24,4 |
|
6 7 8 9 10 11 12 |
Низкий уровень |
22,1 18,9 14,3 18,4 20,8 22,5 24,3 |
22,5 16,4 18,3 17,6 21,0 22,3 21,8 |
21,5 20,3 22,8 24,6 20,8 23,9 22,5 |
24,6 21,4 20,7 23,2 21,4 22,8 20,9 |
23,8 21,9 20,5 22,4 19,3 23,1 22,3 |
|
13 14 15 |
Классифицируемые предприятия |
20,8 18,9 26,4 |
19,3 14,6 22,3 |
24,5 23,6 22,5 |
25,5 28,7 18,0 |
30,1 29,4 27,0 |
Задача №2. При оценке эффективности деятельности предприятий одной из отраслей промышленности получены три класса предприятий: с высоким уровнем эффективности производства, средним и низким. Используя данные следующей таблицы, произведите классификацию двух последних предприятий.
|
№ |
Уровень эффективности |
Показатель |
||
|
Рентабельность, % |
Удельный вес потерь от брака, % |
Производительность труда, тыс.руб./чел. |
||
|
1 2 3 4 5 |
Высокий |
20,1 22,6 24,5 23,1 19,8 |
0,38 0,54 0,21 0,69 0,18 |
160,5 155,4 143,8 178,9 195,4 |
|
6 7 8 9 10 |
Средний |
18,2 14,7 13,8 12,1 11,3 |
0,35 0,45 0,36 0,24 0,59 |
148,6 151,2 150,8 168,2 132,7 |
|
11 12 13 14 |
Низкий |
11,4 11,0 10,9 9,3 |
0,90 0,87 0,53 0,41 |
120,8 119,3 102,8 134,1 |
|
15 16 |
Классифицируемые предприятия |
11,6 18,8 |
0,15 0,88 |
155,1 145,9 |
2. Кластерный анализ.
Задача кластерного анализа состоит в разбиении исходной совокупности объектов на группы схожих, близких между собой объектов. Эти группы называют кластерами или таксонами.
Другими словами, кластерный анализ объединяет различные процедуры, используемые для проведения классификации. В результате проведения этих процедур исходная совокупность объектов разделяется на группы (классы) схожих между собой объектов, обладающими свойством плотности, формой, размером.
В настоящее время известно огромное число алгоритмов кластеризации. Их разнообразие объединяется не только разными вычислительными методами, но и различными концепциями, лежащими в основе кластеризации.
Сложность задач кластерного анализа состоит в том, что реальные объекты являются многомерными, то есть описываются не одним, а несколькими параметрами. Кроме того, данные могут носить нечисловой характер.
Распределение объектов по кластерам на однородные в некотором смысле группы должно удовлетворять критерию оптимальности, который выражается в терминах расстояния (метрики) между любой парой объектов рассматриваемой совокупности.
В целом методы кластеризации делятся на агломеративные (агломерат - скопление) и итеративные девизивные (division - деление, разделение).
Если признаки приведены в
разных единицах измерения, то требуется их предварительная нормировка – такое
преобразование исходных данных, которое переводит их в безразмерные величины.
При обычной стандартизация вычитается среднее и производится деление на корень
квадратный из дисперсии. Полученные в результате стандартизации переменные
имеют нулевое среднее и единичную дисперсию.
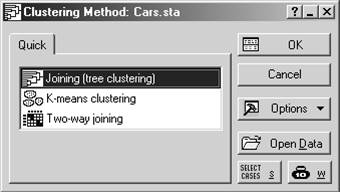
В модуле Кластерный анализ (Cluster Analysis) пакета реализуются следующие методы кластеризации:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.