Расчёт дисперсии, плотности вероятности и функции распределения гармонического сигнала, страница 4

Плотность вероятности для суммы гармонического сигнала и нормального стационарного шума с нулевым средним равна:

,

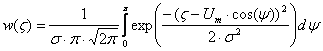где ,

где  - гармоническое колебание с равномерно распределенной начальной фазой,

 - нормальный стационарный шум с нулевым средним.

Введем нормированную случайную переменную: .

.

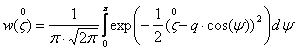Построим график плотности вероятности:

-      отношения сигнал/шум , график плотности вероятности приведен на рис. 10.

.

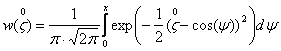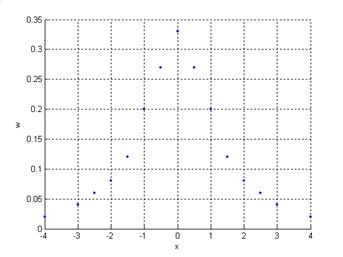
Рис. 10. Графики плотностей вероятности ().

-      отношения сигнал/шум , график плотности вероятности приведен на рис. 11.

.

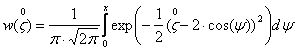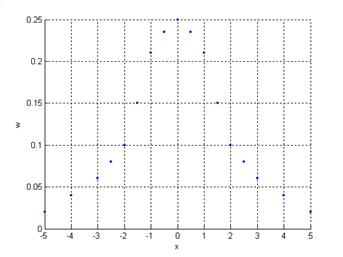
Рис. 11. Графики плотностей вероятности ().

Литература

1.        Гоноровский И.С. РТЦиС. М.: Радио и связь, 1986 г.

2.  Баскаков С.И. РТЦиС. М.: Высшая школа, 2000 г.

3.  Баскаков С.И. РТЦиС. Руководство к решению задач М.: Высшая школа, 1987 г.

4.        Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся ВТУЗов. М.: Государственное издательство физ.‑мат. литературы, 1962г.

5.        Тихонов В. И. Статистическая радиотехника. М.: Советское радио, 1966 г.

6.        Левин Б. Р. Теоретические основы статистической радиотехники. Ч. 1. М.: Советское радио, 1974 г.